アナログオシロスコープを使って複素平面を表現する:今岡通博の俺流!組み込み用語解説(20)(1/2 ページ)
今岡通博氏による、組み込み開発に新しく関わることになった読者に向けた組み込み用語解説の連載コラム。第20回は、三角関数の微分/積分など交流回路の本質にたどりつく上で必要になる複素数の概念の理解に向けて複素平面を取り上げる。
はじめに
連載第14回、第15回、第17回、第18回でコンデンサーやコイルを用いて微分/積分を理解するための記事を書きましたが、実は説明しきれていない部分がありました。
それは、正弦波(sin)を微分すると余弦波(cos)になり、また逆に余弦波を微分すると正弦波になる現象です。積分に関しても同じで、正弦波が余弦波になり、余弦波が正弦波になります。アナログ回路で交流が関わる場合には、これらのような三角関数の微分と積分による変換が必要になりますが、その本質にたどりつくには複素数の概念を理解しなければならないのです。
筆者の記事は電気/電子を系統的に学んだ理系出身の技術者ではなく、このあたりにはあまり明るくはないが組み込みの世界に入ってきた技術者を対象としています。筆者の記事のモットーは、数式を使うことなくアナログ回路やそこで起こるさまざまな現象の理解を手助けすることにあります。
そこで複素数の理解に向けて今回は複素平面を取り上げます。数式は出てきませんが、アナログオシロスコープを使うことで視覚的に複素数を理解するというのがこの記事の趣旨です。
複素数とは
普段私たちが使っている普通の数(実数)は、「数直線」という1本の線の上に置くことができます。0から右へ1、2、3と進み、左へ−1、−2、−3と進む、「1つの次元」しか持っていません。しかし、複素数は、この数直線のルールから飛び出した数なのです。
複素数は、2つのパート、あるいは2つの独立した情報を持っています。
- 実数パート(普通の数):従来の数直線上を動く部分
- 虚数パート(新しい数):従来の数直線と垂直に交わる、全く新しい方向への動きを示す部分
地図で例えるなら、「実数パート」が東西(横)の移動距離を示すのに対し、「虚数パート」は南北(縦)の移動距離を示します。
複素平面
複素平面とは、この「東西南北」の2つの情報を持つ複素数を、1つの点として示すための平面の地図です。従来の数直線を横向きに置き、これを「実軸(実数パートの方向)」と呼びます。これと垂直に交わる新しい線を縦向きに置き、これを「虚軸(虚数パートの方向)」と呼びます。これら2つの軸を持つ平面全体が「複素平面」です。
2現象オシロスコープを用意する
今回の実験では、連載第19回「年代物のアナログオシロでベクタースキャンディスプレイを再現する」で使用したアナログオシロスコープ「KENWOOD CS-4025」を用いて複素平面を表示します(図1)。
本来オシロスコープは横軸を時間、縦軸を信号強度(電圧)で使うのが一般的です。図1はその典型的な使い方を示したものです。
しかし2現象(いわゆる入力チャンネルが2つあり、その波形を1つの画面に表示して比較することができる)のオシロスコープには、モードを「X-Y機能」に切り替えて使えるものがあります。
このX-Y機能では、X軸を時間軸として使用するのではなく、チャンネル2の入力を表示できます。ちなみにY軸は従来通りチャンネル1の入力が表示されます。
オシロスコープに映し出す複素平面の画面構成
図2は、オシロスコープに映し出す複素平面の画面構成を表しています。
複素数は、実数パートと虚数パートで表現されますが、先ほどの複素平面の説明にならって、東西に当たる実数パートは横軸(X)とし、南北に対応する虚数パートは縦軸(Y)とします。
Copyright © ITmedia, Inc. All Rights Reserved.
組み込み開発の記事ランキング
- パナソニックの弱いロボット「NICOBO」がLLMでさらなる進化、累計販売は1万体に
- ソニーがSTB不要のデジタルサイネージを提案、AIデジタルヒューマンも組み込める
- Rapidusの顧客獲得が進捗、60社以上と協議中で約10社にPDKをライセンスへ
- あなたの家電がサイバー攻撃の踏み台に? 購入時は星マークをチェックしよう
- 家電のノジマがロボットショールームにヒューマノイドや業務用を展示する理由
- 製造業の「SBOM」は誰が構築し運用/管理すべきか【後編】
- スバルが制御統合ECU向けマイコンにインフィニオンの「AURIX TC4x」を採用
- チップレットでASIL Dを支援する車載SoC技術を開発
- 出荷量1.3倍を実現、電源不要のIoTゲートウェイが南種子町にもたらす農業改革
- 一度の顔登録で複数サービス利用可能 NECの顔認証基盤、トライアルなどで実証導入へ
コーナーリンク

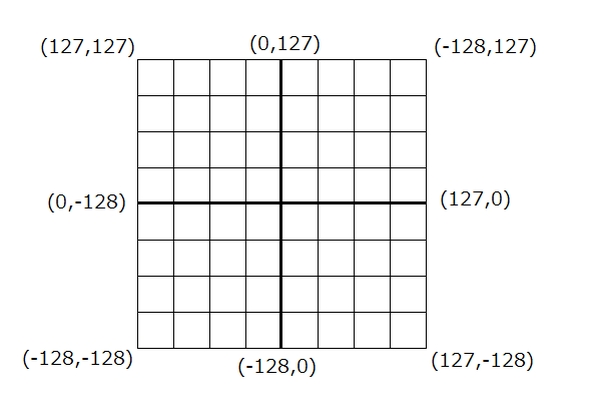 図2 オシロスコープに映し出す複素平面の画面構成
図2 オシロスコープに映し出す複素平面の画面構成

