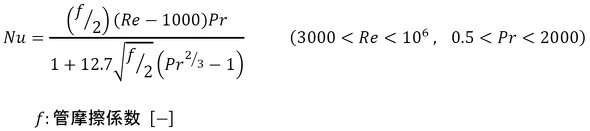円管内の熱伝達を解析する:CAE解析とExcelを使いながら冷却系設計を自分でやってみる(14)(3/4 ページ)
» 2025年08月18日 08時00分 公開
[高橋良一/RTデザインラボ 代表,MONOist]
円管層流熱伝達のシミュレーション
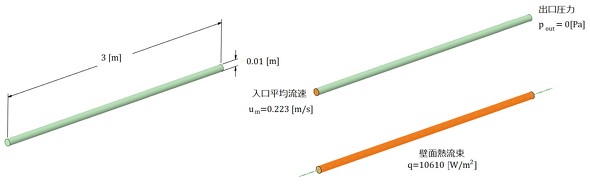
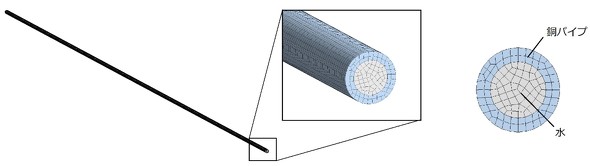
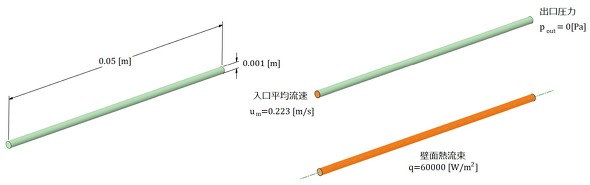
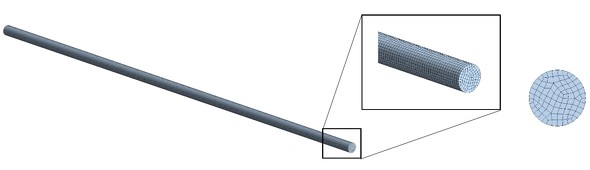
それでは、熱流体解析を進めていきましょう。図3に境界条件を、図4にセル分割図を示します。使用するモデルは、連載第10回と同じものです。
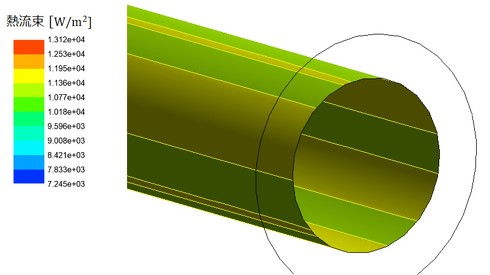
図5に温度分布を、図6に熱流束分布を示します。熱流束分布については、設定した境界条件がそのまま反映された結果となっています。
なお、紙と鉛筆による計算結果とシミュレーション結果との比較は、次項の円管乱流熱伝達を説明した後に行うことにします。
円管乱流熱伝達
円管の乱流熱伝達率の見積もりには、実験式を用います。ここでは、代表的なものを2つ紹介します。式12はディタス・ベルター(Dittus-Boelter)の式です(参考文献[1])。
続いて、式13はグニーリンスキー(Gnielinski)の式です(参考文献[1])。
円管乱流熱伝達のシミュレーション
それでは、熱流体解析を進めていきましょう。図7に境界条件を、図8にセル分割図を示します。使用するモデルは、連載第13回と同じです。
図9に温度分布を、図10に熱流束分布を示します。熱流束分布については、設定した境界条件がそのまま反映されています。
Copyright © ITmedia, Inc. All Rights Reserved.
Special ContentsPR
特別協賛PR
スポンサーからのお知らせPR
Special ContentsPR
Pickup ContentsPR
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
Special SitePR
あなたにおすすめの記事PR



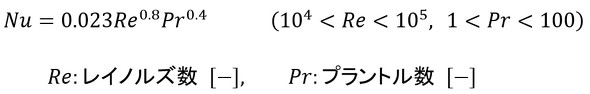 式12
式12