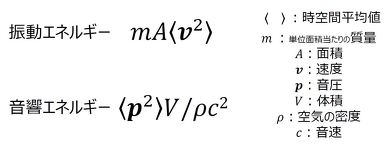フローで考える音振動のモデリング(その1) 〜音振動をエネルギー視点で捉える〜:1Dモデリングの勘所(34)(2/3 ページ)
背景となる理論
背景となる理論であるSEAの考え方を拡張し、1Dモデリングに適用する。以下、その考え方を簡略に示す。なお、SEAに関する理論の詳細については参考文献[1][2]を、実用的な方法については参考文献[3]を、理論の概要については参考文献[4]を参照されたい。
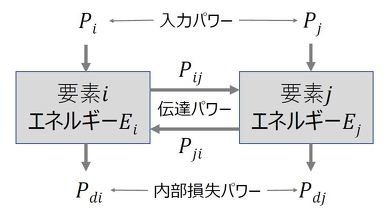
図3に、要素間のパワーのフローを示す。図2の任意の2要素を抽出したものと考えていただきたい。各要素にパワーが入力され、その一部が内部損失で消費され、残りが周囲の要素に伝達する様子を示している。このとき、要素i、要素jの定常状態でのパワーの入力と出力が等しいことから、
が成り立つ。このとき、中心周波数ω、帯域幅Δωの周波数域を考えると、内部損失パワーは以下で表現できる。
ηiは要素iの、ηjは要素jの内部損失係数である。これは、今までに何度か出てきた材料の損失係数と同じである。
一方、要素間の正味のパワーPij−Pjiは、対象とする周波数域のモード数をNiとすると、モード当たりの要素エネルギーEmi=Ei/Niの差に比例する。すなわち、モード当たりのエネルギーの高い方から低い方にパワーは流れる。これは、熱で温度の高い方から低い方に熱量が流れるのと同じ理屈である。
このとき、
で、相反定理ηijNi=ηjiNjを考慮している。上式から、
となり、ここでのηij、ηjiは要素i、要素j間の結合損失係数である。なお、上式にはモード数Niの影響は陽には表れない。モード数の影響は結合損失係数ηij、ηjiに陰に含まれていることに留意されたい。
以上から、パワーの平衡式(電流則に相当)は、
となり、パワーとエネルギーの関係は、
となる。そして、上式を統合して、
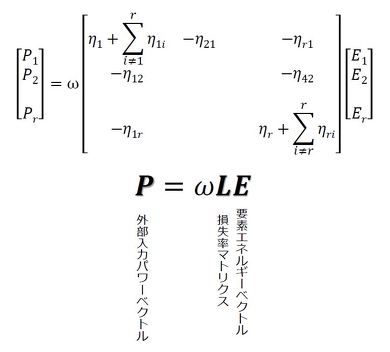
となる。以上は2要素の場合であったが、一般的な多要素の場合には図4のようにマトリクス表示できる。この連立方程式を、Pを入力とし、損失ηを決めて解くことにより、各要素のエネルギーEを求める。単に連立方程式を解くだけなので「Excel」でも解ける。
SEAは、各要素の共振点が多数近接して存在する高周波数域の応答を、要素の空間平均、周波数平均により、エネルギーに変換する方法で、構造要素のエネルギー、音場要素のエネルギーは図5で定義される。すなわち、各要素のエネルギーを知ることによって、振動速度、音圧の時空間平均値を求めることができる。
参考文献:
- [1]R.H.Lyon|Statistical Energy Analysis 2nd Edition
- [2]L.Heckl|Structure Borne Sound|Springer
- [3]入江良彦|SEA法による固体伝搬音解析|日本音響学会誌 48巻6号(1992)
- [4]大野進一、山崎徹|機械音響工学|森北出版(2010)
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 義手とロボットの手を共通化するPSYONICのバイオニックハンド「Ability Hand」
- 同じ機械なのに1号機はOK、2号機はNG 設計者を悩ませる“再現しない不具合”
- 高精度3Dスキャナー3機種を発売、自動検査や医療分野を支援
- 約3.5kgの力で打ち抜ける手動式卓上パンチプレス
- 製造業の情報を一元管理するDXプラットフォームの体験型施設を開設
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 令和版の健康サンダル? 否、感覚を増幅する「Nike Mind」が気になる件
- 新型コロナで深刻なマスク不足を3Dプリンタで解消、イグアスが3Dマスクを開発
- 幾何公差の基準「データム」を理解しよう
- 強度設計の出発点 “計算”より先に考えるべきこととは?
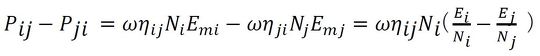 式3
式3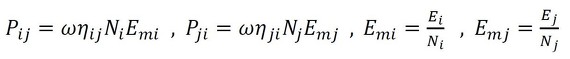 式4
式4