フローで考える熱のモデリング(その1) 〜熱の理論と熱回路網解析〜:1Dモデリングの勘所(31)(3/4 ページ)
» 2024年05月16日 09時00分 公開
[大富浩一/日本機械学会 設計研究会,MONOist]
熱伝導の基本問題
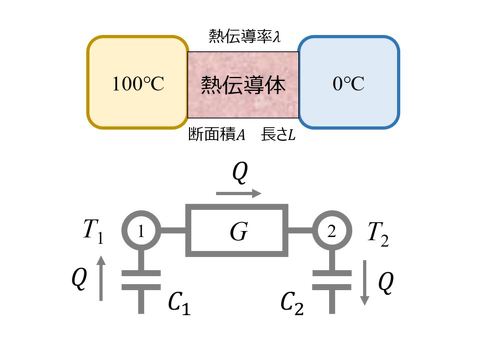
以上の知見を基に、図4上図に示す熱伝導の基本問題を考える。100℃の物体と0℃の物体があり、両者を熱伝導体で接続した後の、熱量の移動、各物体の温度を求める問題である。
図4上図を図1の考え方にのっとって熱回路網で表現すると図4下図となる。熱伝導体の熱コンダクタンスをG[W/K]、各物体の熱容量をC1、C2[J/K]、温度をT1、T2[℃]、熱量をQ[W]とする。熱量は図の矢印の方向を“正”とする。このとき、以下の式が成立する。
上記第1式の両辺を時間tで微分し、この式に第2式と第3式を代入すると、
となる。この式を、t=0でT1=T10、T2=T20、Q=G×(T10−T20)≡Q0という条件の下で積分すると、
となる。この式を最初の第2式、第3式に同様の手順で代入すると、
となる。なお、t→∞の場合、
となる。すなわち、十分に時間が経過すると両者の温度は同じになり、その温度は両者の初期温度と熱容量で決まる。
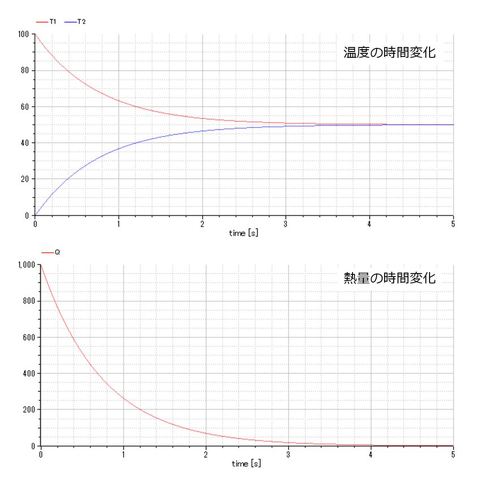
上記の熱伝導の基本問題をG=10、C1=C2=15として結果を図示すると図5となる。熱容量が物体1と物体2で同じなので、温度は両者の温度の中間値である50℃に収束していることが分かる。一方、熱量は両者の温度差が小さくなるにしたがって減少し、最終的にゼロ(熱平衡)になる。
本問題は式を直接「Modelica」テキスト表現して数値的に解くこともできる。結果は当然図5と同じになる。Modelicaテキスト表現の例を以下に示す(リスト1)。
model twoMasses Real T1 (start=100); Real T2 (start=0); Real Q; parameter Real G=10; parameter Real C1=15; parameter Real C2=15; equation Q=-G*(T2-T1); der(T1)=-Q/C1; der(T2)=Q/C2; end twoMasses;
リスト1 Modelicaでテキスト表現した場合
Copyright © ITmedia, Inc. All Rights Reserved.
Special ContentsPR
特別協賛PR
スポンサーからのお知らせPR
Special ContentsPR
Pickup ContentsPR
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
Special SitePR
あなたにおすすめの記事PR
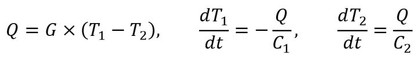 式17
式17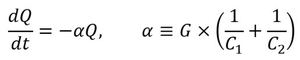 式18
式18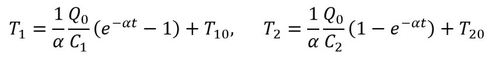 式20
式20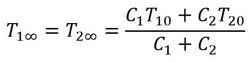 式21
式21