フローで考える熱のモデリング(その1) 〜熱の理論と熱回路網解析〜:1Dモデリングの勘所(31)(2/4 ページ)
熱伝導の式
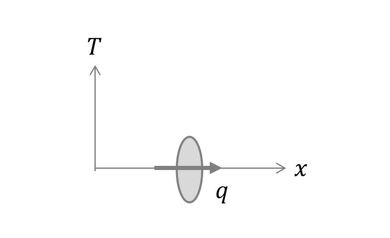
ここで、熱をその理論に立ち返って考えてみる。図2に示す物質内のある位置において、「熱伝導」によって伝わる熱の移動量はその位置の温度勾配に比例することが実験的に分かっており、式6で表せる。
q[W/m2]は単位時間、単位面積当たりの熱量で「熱流束」と呼ばれる。λ[W/m・K]は熱伝導率で物質によって決まる物性値である。上式から、断面積A[m2]を流れる熱量Q[W]は、
となる。この式と前項の熱コンダクタンスの定義の式から、熱伝導に関する熱コンダクタンスは、
となる。L[m]は熱が流れる方向の物体の長さである。
次に、3次元の熱伝導について考える。図3に示すように、固体の中の微小要素dxdydzなる直方体を考える。
x方向に関して、断面dydzを通して左側から入る熱量[W]は、
となり、右側から出る熱量は、
なので、直方体に蓄えられる熱量は、
となる。同様にしてy方向、z方向に関して(図には示していないが)、
となる。以上から、この直方体に蓄えられる熱量は下記となる。
今、この固体の定圧比熱をc[J/kgK]、密度をρ[kg/m3]とすると、この微小要素の温度を1℃上げるのに必要な熱量(エネルギー)はρcdxdydzとなる。「比熱」とは、その単位から分かるように、物質ごとに異なる値を有し、その物質1kgの温度を1℃上げるのに必要なエネルギーの量である。上記の微小要素に蓄えられた熱量によって、時間dtの間に、微小要素の温度がdT上昇することになるので、
となる。左辺[]内のw[W/m3]は単位時間、単位体積当たりの内部発熱量である。この右辺の熱量に関する式と前項の熱容量に関する定義式から、熱容量は、
となる。V[m3]は物体の体積である。前々式は最終的に、
となる。α≡λ/ρcは、温度伝導率(熱拡散率)である。上式が3次元の熱伝導方程式である。
図3の熱伝導方程式を解くことにより、物体内の温度分布と時間変化が求まる。温度が求まると図2の熱伝導の基本式から熱流束の大きさや熱量の方向が計算できる。すなわち、熱伝導方程式は温度(ポテンシャル)に関する式で、熱の流れ(フロー)はそれに従属した形式で求まる。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
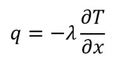 式6
式6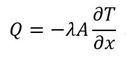 式7
式7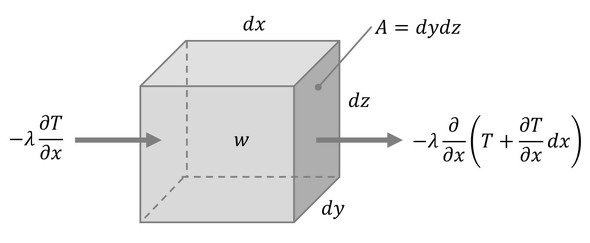
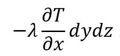 式9
式9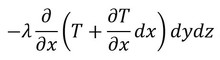 式10
式10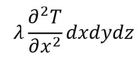 式11
式11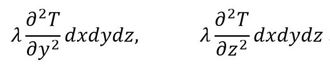 式12
式12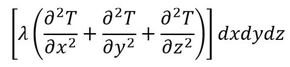 式13
式13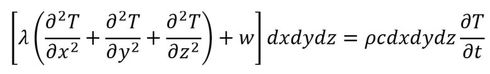 式14
式14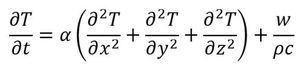 式16
式16





