スピーカーのモデリング〜電気、機構、音響の連成問題、3つの現象を回路で表現〜:1Dモデリングの勘所(12)(3/5 ページ)
» 2022年10月18日 09時00分 公開
[大富浩一/日本機械学会 設計研究会,MONOist]
スピーカー全体のモデリング
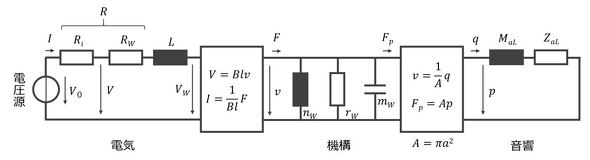
以上、導出した電気回路、機構回路、音回路をまとめると、図7のように全体表現できる。電気回路の出力が機構回路の入力に、機構回路の出力が音回路の入力になっている。
図7の状態では解くことが困難なので、電気回路と音回路を機構回路に縮約することにする。最初に、音回路を機構回路に縮約する。具体的には、音響回路の音響摩擦ZaLと音響マスMaLを、機構回路のマスと摩擦インピーダンスに等価な等価マスmL、等価インピーダンスrLに変換する。このためには、表1の変数と要素の関係式および機構→音の変換式を利用する。すなわち、
となる。さらに、電気系の電圧源を「オームの法則」により電流源に変換する。その際、コイルのインダクタンスの影響は抵抗に比べて小さいものとして無視する。
以上の結果を図8上図に示す。
次に、電気回路を機構回路に縮約する。音回路→機構回路と同様の考え方により、電気回路の等価摩擦インピーダンスrelと、力源F0は次式で表現される。
以上から、音回路、電気回路を機構回路に縮約した回路は図8下図となる。
参考文献:
- [2]A. Lenk, R.G.Ballas, R.Werthschützky, and G.Pfeifer, Electromechanical Systems in Microtechnology and Mechatronics, Springer, 2011
Copyright © ITmedia, Inc. All Rights Reserved.
Special ContentsPR
特別協賛PR
スポンサーからのお知らせPR
Special ContentsPR
Pickup ContentsPR
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
Special SitePR
あなたにおすすめの記事PR
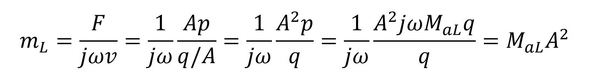 式7
式7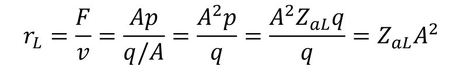 式8
式8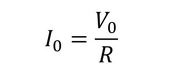 式9
式9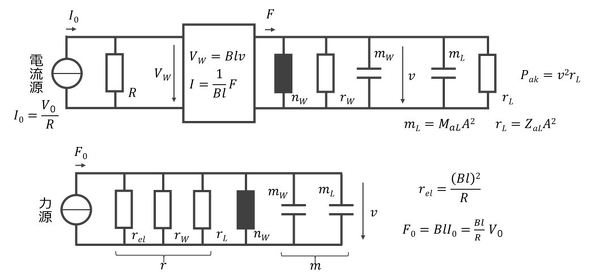
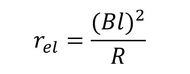 式10
式10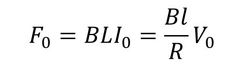 式11
式11





