固有振動数解析の流れを“ステップ・バイ・ステップ”で理解する：構造解析、はじめの一歩（6）（3/3 ページ）

[栗崎 彰／サイバネットシステム シニア・スペシャリスト，MONOist]

結果を観る

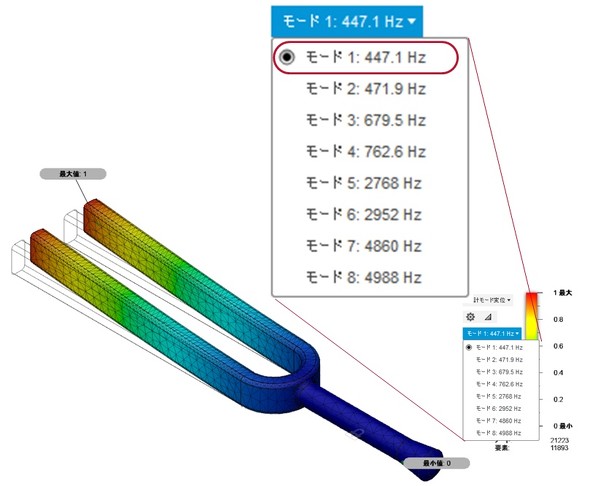
　固有振動数は、多数存在します。1つ目の固有振動数を「1次固有振動数」といいます。以下同様に、2次、3次と続きます。

　一番注目すべきなのは、1次固有振動数です。この固有振動数で共振が生じた場合、構造は大きなダメージを受けます。まずは1次固有振動数が、「魔の周波数領域」に入っていないかどうか確認しましょう。

　音叉の1次の固有振動数は、「447Hz」となりました（図3）。「ラ」の振動数である440Hzに極めて近い結果となっています。

図3　音叉の固有振動数解析結果（1次） ［クリックで拡大］

　変形図のような図は、1次の揺れ方を表したものです。「モード形状」や「モードシェイプ」といいます。

　ここで気を付けなければならないのは、この変形は「絶対量ではない」ということです。最大変形ポイントを「1」とした場合の「相対変形量」です。この「1」は「1mm」ではありません。

　使用するソフトによっては、この相対変形量を基に応力図を描くものがあります。しかも、単位が「MPa」などともっともらしく出てきてしまうので、絶対的な応力と勘違いしてしまう場合があります。固有振動数解析から応力は出ません。求まるのは、固有振動数と最大変形量を「1」とした相対変形量であるモードシェイプです。よく覚えておいてください。

　これが固有振動数解析の流れになります。ポイントは、（1）密度を指定することと、（2）モードシェイプは相対変形量であるということです。

部品の弱点を見つける

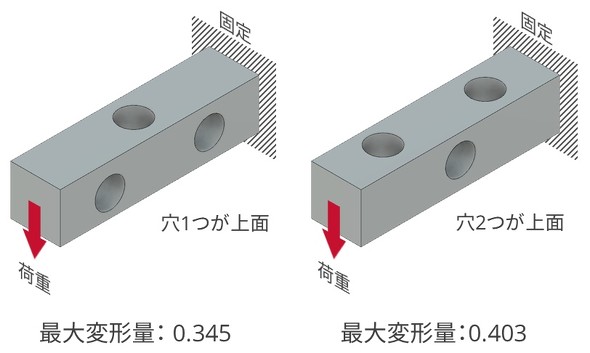
　図4に示すような部品があるとします。一方が固定されており、もう一方に鉛直方向に荷重がかかります。穴が2つある面を上面にするのと、側面にするのと、どちらの方が構造的に有利でしょうか。

図4　単純な部品の配置方向と強度（線形静解析結果） ［クリックで拡大］

　それぞれに対し、線形静解析をして変形量を見てみれば分かることです。その結果、穴2つを側面になるように配置した方が、構造的に有利であることが分かりました。

　固有振動数解析を行うことによって、部品の弱点が分かります。

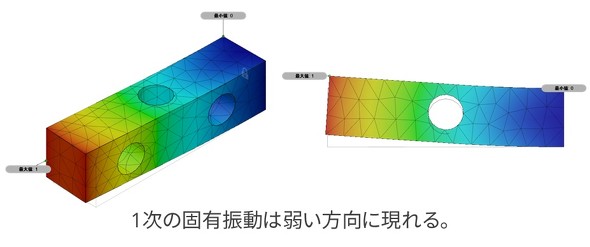
　同じモデルについて、固有振動数解析を行った結果が図5です。1次固有振動数のモードシェイプを見ると、穴が2つある面が面外に曲がるような変形となっています。弱い方向に1次固有振動が現れるのです。これは線形静解析の結果と一致します。また、単純な形状の部品の配置を決める際にも固有振動数解析は使えます。（次回に続く）

図5　固有振動数解析で分かる部品の弱い方向（固有振動数解析結果） ［クリックで拡大］

コラム

先日、サイバネットシステムでオンラインセミナーを開催しました。通常なら皆さんに集まっていただいて開催するセミナーなのですが、世の中の状況が状況なのでオンライン形式としました。

オンライン配信そのものに慣れていないせいか、いろいろと苦労しました。画面が暗い、音声が小さい、露出がモニターに合ってしまってプレゼンターが真っ黒……。何事もやってみないと分からないものです。

普段、何気なく見ているYouTubeですが、YouTuberの方々は本当にいろいろな工夫をされているのですね。彼らの努力が身に染みて分かったイベントでした。

そして、得た教訓。「やってみないと本質的なことは分からない」。

これはCAEにも通じることだと思います。

⇒ 連載バックナンバーはこちら

Profile

栗崎 彰（くりさき あきら）

1958年生まれ。サイバネットシステム株式会社 シニア・スペシャリスト。1983年より37年間、構造解析に従事。I-DEASの開発元である旧 SDRC 日本支社、CATIAの開発元であるダッソー・システムズを経て現在に至る。多くの企業で3次元CADによる設計プロセス改革コンサルティングや、設計者解析の導入支援を行う。特に設計者のための講座「解析工房」が人気。解析における最適なメッシュ・サイズを決定するための「OK法」を共同研究で模索中。