データムはどうやって決めるの? 3D CADで考えよう:3D設計推進者の眼(34)(3/3 ページ)
寸法(サイズ)公差と幾何公差
前回お話したように、現在では3D CADと連携可能な便利な公差計算・公差解析ツールがあります。これらのツールでは、設定された寸法(サイズ)公差があれば公差計算を行うことが可能です。
これまでの公差計算・公差解析のお話では、寸法(サイズ)公差についてのみ取り扱い、公差計算を行う上で、互換性の方法と不完全互換性の方法での計算事例や、公差計算・公差解析ツールでの運用事例について説明してきていますが、この幾何公差もまたこれらの公差計算・公差解析で利用することから、以前お話しした正規分布や工程能力指数と同じように、「オペレーションやツール論ではなく、まずは理論を理解する」ということが重要ということをお話してきています。
実はこの幾何公差は、「レバー比」「感度」といわれるものとして、公差計算・公差解析に影響を持ちます。このレバー比については、公差計算・公差解析のプロフェッショナルであり、先駆者でもあるプラーナー(PLANER)の会長である栗山弘氏、社長の栗山晃治氏より私はこれまで学んできています。
このレバー比については、次回以降で詳しくお話しすることとしますが、もしかしたら、皆さんの中には、
「寸法(サイズ)公差と幾何公差が記された図面の解釈は?」
「どう寸法(サイズ)公差と幾何公差を同一の形体に対して設定するのか? 取り扱うのか?」
と迷われてしまう人がいるのかもしれません。私もどう扱うべきか悩みました。
このモデルで、第1次データム平面Aとその平面Aから10mmの距離にある面は寸法(サイズ)公差と幾何公差によってどのような拘束を付けられているのでしょうか。第1次データム平面Aは平面度公差域0.02mmにあります。
第1次データム平面Aと寸法(サイズ)公差10±0.2mmのという間隔(距離)にあると設定された面は、データム平面Aに対して0.05mmの大きさの平行度公差域にもあります。
もう少し詳細に説明します。寸法公差(サイズ)公差により、この面の間隔(距離)は9.8mmから10.2mmまで許容されています。しかし、平行度はこの寸法(サイズ)公差として許容されている大きさに比べて4分の1も小さな0.05mmとなっています。
この数字だけを見ると、あまりに数字の大小があったので、私自身、混乱しました。しかし、この解釈は次のようにします。「この面の間隔は9.8mmから10.2mmまで許容されるが、平行度は0.05mm以内でなければならない」。つまり、「寸法(サイズ)公差と幾何公差は一緒に考える・設定するのではなく、別々のものとして取り扱う」というように私の言葉としては表します。
このことを「独立の原則」と言い、JISにも定義されています。
JIS B0024-1988(ISO 8015-1985)抜粋「独立の原則」
図面上に個々に指定した寸法及び幾何特性に対する要求事項は,それらの間に特別の関係が指定されない限り,独立に適用する。それゆえ何も関係が指定されていない場合には,幾何公差は形体の寸法に無関係に適用し,幾何公差と寸法公差は関係のないものとして扱う。
したがって,もし,
- 寸法と形状又は
- 寸法と姿勢又は
- 寸法と位置
との間に特別な関係が要求される場合には,そのことを図面上に指定しなければならない。
この独立の原則も公差計算・公差解析を学ぶ中で教えていただいた内容でした。当時、私は設計者としてはまだまだ未熟ではありましたが、あらためて定義を学ぶ中で、その認識ができたように思えます。
案外この独立の原則を説明できる人は多くはないかもしれません。これにより、幾何公差は、公差計算・公差解析を行う上で、寸法公差とは別に影響があるものとして、独立した別のパラメータとして計算することができると私は理解しています。
包絡面、包絡の条件
さらに、この独立の原則ですが、私にとっては難しい説明を加えることができます。「包絡面」「包絡の条件」はご存じでしょうか。包絡面のお話をしようとすると「最大実体寸法(サイズ)MMS:maximum material size」のお話しもしていかなければなりません。
MONOistの連載「製図を極める! 幾何公差徹底攻略」で山田学氏(ラブノーツ/六自由度技術士事務所)が独立の原則と包絡面に関して、また包絡の条件について詳細の説明をされていますので、ぜひお読みください。
ここでは、包絡の条件とは、独立の原則とは逆に、「寸法(サイズ)公差と幾何公差を一緒に取り扱う」というお話に留めますが、公差設計・公差解析のお話を進める中で、幾何公差を設定する時に大きな効果を得ることが期待できる「最大実体公差方式」のお話をする機会にあらためてお話したいと思います。
幾何公差は、現在GD&T(幾何公差設計法)というものが主流となるべく動いている中で、学んでいくべきことが多くあります。
さて次回は公差計算・公差解析における幾何公差のレバー比(感度)のお話をします。お楽しみに。(次回に続く)
関連記事
 幾何公差の基準「データム」を理解しよう
幾何公差の基準「データム」を理解しよう
データムの配置位置の仕方には、さまざまなルールがあるので要注意。あなたの作成した過去図面は大丈夫? 「データム記号」の使い方と設計者が身に付けておくべき作法
「データム記号」の使い方と設計者が身に付けておくべき作法
機械メーカーで機械設計者として長年従事し、現在は3D CAD運用や公差設計/解析を推進する筆者が公差計算や公差解析、幾何公差について解説する連載。第5回はデータム記号の使用方法を説明する。 データムはどうやって決めるの? 3D CADで考えよう
データムはどうやって決めるの? 3D CADで考えよう
機械メーカーで3D CAD運用や公差設計/解析を推進する筆者から見た製造業やメカ設計の現場とは。今回は具体的にデータムとは何により決められているのかを説明する。 データムを必要とする幾何公差【その1】〜姿勢公差の平行度〜
データムを必要とする幾何公差【その1】〜姿勢公差の平行度〜
機械メーカーで機械設計者として長年従事し、現在は3D CAD運用や公差設計/解析を推進する筆者が公差計算や公差解析、幾何公差について解説する連載。第8回はデータムを必要とする幾何公差をテーマに、姿勢公差の平行度について取り上げる。 データムを正しく使えていますか?
データムを正しく使えていますか?
アイティメディアがモノづくり分野の読者向けに提供する「MONOist」「EE Times Japan」「EDN Japan」に掲載した主要な記事を、読みやすいPDF形式の電子ブックレットに再編集した「エンジニア電子ブックレット」。今回は人気記事「幾何公差の基準「データム」を理解しよう」をお届けします。 「データム」とは何か? をあらためて理解する
「データム」とは何か? をあらためて理解する
「データム(Datum)」とは? 今回は、設計者であれば当たり前のように聞くこの用語について掘り下げていきます。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
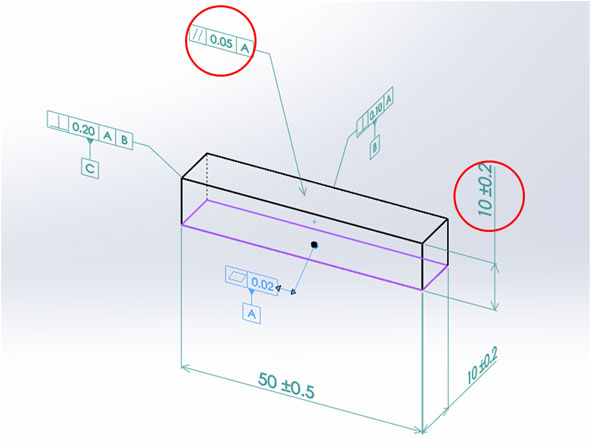 寸法(サイズ)公差と幾何公差
寸法(サイズ)公差と幾何公差







