原価低減に欠かせない科学的アプローチを学ぶ【後編】:実践! IE;磐石モノづくりの革新的原価低減手法(9)(3/5 ページ)
ワークサンプリング法の誤差
絶対誤差と相対誤差
誤差を「物差し」を例に考えてみると、「物差し」の長さの正確さを現す方法に次の2通りが考えられます。
- (ア)この「物差し」の誤差は、±a cmである。
- (イ)この「物差し」の精度は、±b %である。
「物差し」の長さを“L”とすれば、b%=(a÷L)×100 となります。また、(イ)のように“b%”と表現すれば、あえて全長“L”を示さなくても正確さの程度を判断することができます。(ア)の表現を「絶対誤差」、(イ)の表現を「相対誤差(または、精度)」といいます。
「ワークサンプリング法」においても2つの誤差が考えられます。観測回数を多くすればするほど、求める比率(P)は前述した通り正確さは増していきますが、観測結果である比率の用途によってはそれほどの正確さを必要としない場合も多くあります。この許容される誤差を、先の関係式 b%=(a÷L)×100 を変形して「相対誤差(S)」と「絶対誤差(E)」で表すと E=S×P となります。
ワークサンプリング法における“観測回数N”を決めるためには、特段の理由のない限り信頼度95%になるように調査を行うのが一般的です。すなわち「絶対誤差(E)」を標準偏差の2倍とすると以下の通りとなります。
正規分布
例えば、長さ20cmに切断した50枚の鉄板の長さを実際に測定してみると、全く同じ長さの鉄板は少なく、その測定結果でヒストグラム(度数分布図)を描いてみると、左右対称で山型状の形をした分布となります。この例のように物の長さや外径の測定値のような連続量は、ほとんど、この分布に近似することができます。
製品の寸法などは、長いことも短いこともあるので、狙いの寸法に対する誤差はプラス側もマイナス側も同等になり、図示すると左右対称の山型の分布、いわゆる、この連続的な確率分布を「正規分布」と呼びます。また、自然現象の中には、その出現率が「正規分布」をなすものが多く、人間の身長や体重などもこの例に該当します。
「正規分布」は、平均値を示す縦座標の両側に1σ(標準偏差)の領域を取ると、その内の面積は全面積の68.26%、2σでは、95.45%、3σでは、99.73%となります。2σの場合を例にとると、母集団から抽出したデータの95.45%は2σの中に入り、残りの4.55%は2σ外に出ます。すなわち、データの信頼度は約95%であることを意味するといえます。
「ワークサンプリング法」は、確率の法則に基づくもので、母集団から無作為に抜き取った試料は、母集団に似た性質を持ち、さらに試料数を十分に大きくすれば試料の特性分布曲線は母集団の特性分布曲線と極めて近似するということは、先に説明した通りです。
関連リンク
Copyright © ITmedia, Inc. All Rights Reserved.
製造マネジメントの記事ランキング
- 従業員のスキルに応じた「ランク認定制度」も 三菱電機が推進するDX人材育成施策
- 「中国のスペースX」銀河航天は衛星をどう量産するのか 製造デジタル基盤の全貌
- パナソニックは新技術拠点「Technology CUBE」で“実装力のあるR&D”を強化
- 生産性100倍に、富士通がソフトウェア開発をAIエージェントで自動化する開発基盤
- AIエージェントが代わりに働くようになったら人は何をするの?
- 「好きなことは楽しめる間にとことん楽しむ」という考え方の重要性について
- 日本は本当に遅れているのか? AI×現場力で始まる日本型モノづくりの逆襲
- アイリスオーヤマなど、無線制御技術を軸に建設業界の課題解決に向けた協業開始
- IOWN APNと画像認識AIにより、約300km離れた工場での外観検査に成功
- 富士フイルムBIがトルコ企業を買収、基幹システム導入の海外展開加速
コーナーリンク
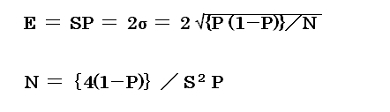
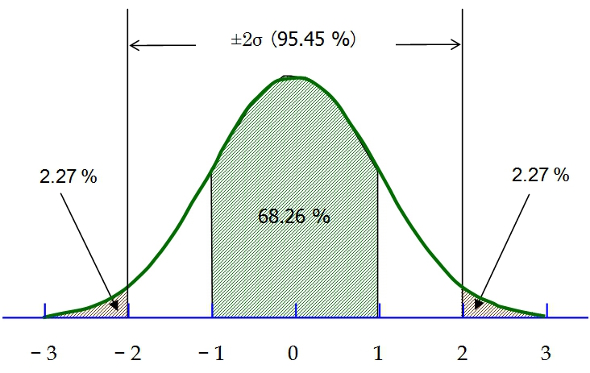 ワークサンプリング法の正規分布の様子
ワークサンプリング法の正規分布の様子



