時間もお金もなくても実践できる信頼性テストの方法とは?:タグチメソッドのデータを解析しよう(1)(2/2 ページ)
1-2.なぜノイズ因子(誤差因子)を重要視するのか
市場の問題は、条件ばらつきが原因で起きる想定外問題
普通の工業製品は、標準的な使用方法を前提に設計されています。従って、設計時に想定していない環境条件で使用されると、いろいろな不具合が発生する可能性があります。例えば環境温度や電源電圧の変動、使用時間や使用方法の違い、新品の場合と劣化した場合などで、条件がばらつくことで不具合現象が発生しやすくなります。
これらの条件が単独に変動しただけでは、大きな不具合にはならないでしょう。しかし幾つかの条件が組み合わさることで、予想外に大きな不具合が起こることが考えられます。
市場における環境は設計時の想定を超えているものです。現在もなおリコール問題が発生し続けているということは、つまり設計時の予想を超える条件が市場に存在することを示しています。
現実の市場の環境は、設計時の予想をはるかに超えている!
つまり市場で発生する製品の不具合とは、設計時に予想した以上に、環境条件や使用条件のばらつきが起こってしまうことによる信頼性問題なのです。
例えばノイズやストレスの影響を考えることは、すなわち市場での信頼性を考えることです。タグチメソッドは市場の信頼性問題を対象にしているため、誤差因子やノイズにこだわります。
タグチメソッドが理解しにくい主な理由
「タグチメソッドが理解しにくい」といわれる理由の1つに、誤差因子またはノイズ因子の存在があります。ご存じのように、実験や試験データには誤差やばらつきが付き物です。だから従来は、多数のデータを用意することで、解析結果にばらつきが影響しないよう工夫したのです。それが大量のデータが要求されていた理由だったはずです。
それなのに、
「なぜばらつきの原因である厄介なノイズ因子をわざわざ取り上げて、さらにそれを大きく変化させてテストするのか? その理由が分からない。そんなことをすれば、ますますデータのばらつきが大きくなり、収拾がつかなくなるだけではないか」
タグチメソッドが理解できないという声には、そんな疑問が含まれているのです。
ばらつきデータにこそ情報が含まれている
ではタグチメソッドで誤差因子(ノイズ因子)を重要視する理由を説明しましょう。この理由を理解することが、タグチメソッドの発想を理解することにつながります。
誤差因子とは、データに誤差やばらつきを生み出す原因のことです。タグチメソッドでは、誤差やばらつきにこそ重要な情報が含まれていると考えます。なぜなら、厳密に考えれば、データに誤差やばらつきが出るのは、本来の動き方からずれているからです。設計で狙った通りの動きをするなら、ばらつきは出ないはずです。狙いと異なる動きになっているから、結果がばらつくのです。つまり設計された本来の働きを乱す原因があるから、データに誤差やばらつきが出るということです。
ですから、誤差やばらつきを解析すれば、本来の働き方からの「ずれ量」が分かるはずで、それを解析すれば、原因の影響をどれだけ受けているかが分かるでしょう。これが、タグチメソッドで誤差因子・ノイズ因子を多用する理由です。
ばらつきは宝の山
ここでは「ばらつきデータこそが宝の山だ」ということを説明しましょう。あるテレビ番組で、中学校や高等学校の教育問題を取り扱っていました。その番組の中で、興味ある例を見つけました。生徒の学力テストの成績分布です。
驚くことに、成績分布のカーブの多くが図1-1のような2つ山になるのだそうです。
生徒の人数が多い場合、成績分布はつりがね形状のきれいな正規分布になるだろうと考えませんか? ところが実際はそうではないのです。
2つ山には理由がある
なぜ成績分布は、2つ山になるのでしょうか。その理由は、番組でも説明していました。「テスト範囲の基本的事項を理解している生徒は平均点が高く分布し、理解していないために平均点が低い生徒との間で、傾向がはっきりと別れてしまうから」なのだそうです。
なるほど、それなら納得できますね。本来、きれいなつりがね形の正規分布とは、データが偶然にばらつく場合、つまりランダムなばらつきを前提にした考え方が基本です。ですから、成績データのようにランダムにならない原因がある場合だと、正規分布にはならないのは当然です。偏った傾向のあるデータでは、左右対称の分布にはならないのです。
このような現象は、学力テストの成績分布だけに限りません。私たちが扱う現実のデータは、むしろ正規分布にならないものが数多くあるのではないでしょうか。むしろ、「その方が普通だ」と考えた方がよいでしょう。
分布の形こそが情報だ
私たちはデータ数が多い場合、安易に正規分布を前提にしてしまいがちです。そういう風に学校で教育をされてきたと言った方が、より正確でしょう。しかし成績分布の例でも分かるように、全くの偶然による現象ではなく、明確なばらつき原因が存在する場合は、いくらデータの数を増やしても1つ山の正規分布にはなりません。
この事実は重要なことを示しています。つまり分布形にこそ、重要な情報が含まれているのです。成績分布が2つ山になったからこそ、「基本事項を理解していない生徒がいる」という有用な情報を得ることができたのです。もし成績の結果が1つ山の正規分布だったら、偶然にばらついただけなので、そのデータからは何の情報も得られません。従って「この次は皆頑張れよ!」と、はっぱを掛けるような対策案しか出てこないでしょう。
正規分布から得られる情報量は少ない
情報工学でいわれるように、分布データが持つ情報量は正規分布が一番少ないのです。いくら大量のデータであっても、正規分布しているデータからは、平均値とばらつきσ(シグマ)以外の情報は何も得られません。しかも、そのばらつきは偶然に支配されているのですから、有効な対策案に結び付きません。
ばらつきこそ宝の山、有用な情報が埋もれている。
だから、ばらつきに正規分布を仮定することは無意味である。
なぜなら、正規分布が持っている情報量が一番少ないから。
現実の問題を解決しようとする技術者なら、正規分布を仮定してはいけません。むしろ正規分布からの外れた方に注目すべきなのです。ばらつきの形こそ、有用な情報を取り出せる宝の山なのです。
データ解析の目的
学力テストの成績分布では、ばらつきが2つ山の形になる事実に重要な情報が含まれていました。ですから教育方法を改善した後に、もう一度テストをしてみて、2つ山の位置や大きさが変化するならば、教育方法の改善は効果があったと分析できます。分布の形、つまりばらつきのデータには、有用な情報が含まれていることが分かります。
では、もう1つの情報である平均値は、どうでしょうか。残念ながら平均値は、試験問題の難易度に左右されます。前回のテストより平均値が下がったとしても、前回より難しい問題だったということなら、生徒の学力に関する重要な情報は含まれていないことになります。つまり成績分布の場合は、2つ山の分離程度を数値化するのが正しい解析法と考えられます。この場合の平均点は、それほど重要な情報ではありません。
この例から分かるように、データのばらつきから必要な情報をいかにして取り出すかが、データ解析の重要項目なのです。
データの解析が目的ではない。データから情報を取り出すことが目的だ
次回は、データから情報を取り出す具体的な方法を解説します。
関連記事
Copyright © ITmedia, Inc. All Rights Reserved.
製造マネジメントの記事ランキング
- 生産性100倍に、富士通がソフトウェア開発をAIエージェントで自動化する開発基盤
- 従業員のスキルに応じた「ランク認定制度」も 三菱電機が推進するDX人材育成施策
- 日本は本当に遅れているのか? AI×現場力で始まる日本型モノづくりの逆襲
- 「好きなことは楽しめる間にとことん楽しむ」という考え方の重要性について
- パナソニックは新技術拠点「Technology CUBE」で“実装力のあるR&D”を強化
- アイリスオーヤマなど、無線制御技術を軸に建設業界の課題解決に向けた協業開始
- IOWN APNと画像認識AIにより、約300km離れた工場での外観検査に成功
- AIエージェントが代わりに働くようになったら人は何をするの?
- 永守氏がニデック完全退任、「経営者としての私の物語にピリオド」
- 富士フイルムBIがトルコ企業を買収、基幹システム導入の海外展開加速
コーナーリンク
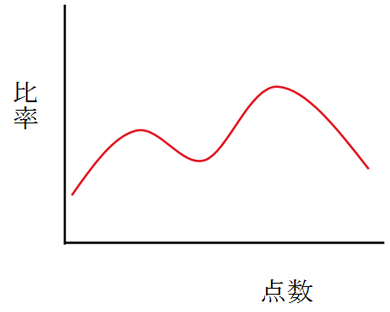 図1-1 実際に多い成績分布の形
図1-1 実際に多い成績分布の形




