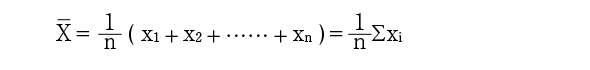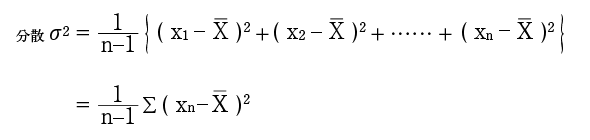ヒストグラムの読み方、コツと経験則:実践! IE:現場視点の品質管理(12)(3/4 ページ)
» 2012年03月30日 11時52分 公開
[福田 祐二/MIC綜合事務所所長,@IT MONOist]
平均値と標準偏差の求め方
このようにデータをヒストグラムにまとめてみると特性値の分布の形がよく分かります。ところが、その形が中心に密集しているとか、左右対称であるとか、幅(広がり)が大きい、というような定性的な評価・表現では、人によって判断が異なります。
そこで、誰もが一定の評価ができるように、これらを数量化して表すようにします。さらに深く分布の形を調べていくには、分布を数量で表す必要があります。
代表的な数値化の例として、平均値は分布の中心的傾向を表し、分散(σ2またはs2)や標準偏差(σまたはs)あるいは範囲(R)はバラツキの度合いを表すときに用いられます。標準偏差の表し方として使用されるギリシャ文字σ(シグマ)は、英文字ではsのことで、標準偏差(standard deviation)の頭文字ですので、どちらも同じ意味で使用されますが、ここではσを用いて説明します。次に、これらの求め方について述べます。
(1)一般的な求め方
一般に、平均値は、次式で求められます。
また、標準偏差(σ)は次式で求められますが、下記の算式で求めた分散(σ2)の正の平方根を標準偏差(σ)と呼びます。
Copyright © ITmedia, Inc. All Rights Reserved.
Special ContentsPR
特別協賛PR
スポンサーからのお知らせPR
Special ContentsPR
Pickup ContentsPR
製造マネジメントの記事ランキング
- 従業員のスキルに応じた「ランク認定制度」も 三菱電機が推進するDX人材育成施策
- パナソニックは新技術拠点「Technology CUBE」で“実装力のあるR&D”を強化
- 生産性100倍に、富士通がソフトウェア開発をAIエージェントで自動化する開発基盤
- AIエージェントが代わりに働くようになったら人は何をするの?
- 「好きなことは楽しめる間にとことん楽しむ」という考え方の重要性について
- 日本は本当に遅れているのか? AI×現場力で始まる日本型モノづくりの逆襲
- 「中国のスペースX」銀河航天は衛星をどう量産するのか 製造デジタル基盤の全貌
- アイリスオーヤマなど、無線制御技術を軸に建設業界の課題解決に向けた協業開始
- IOWN APNと画像認識AIにより、約300km離れた工場での外観検査に成功
- 富士フイルムBIがトルコ企業を買収、基幹システム導入の海外展開加速
Special SitePR
コーナーリンク
あなたにおすすめの記事PR