明石海峡の強風にあおられても、大丈夫?:独学! 機械設計者のための自動制御入門(4)(3/4 ページ)
伝達関数の演算と周波数応答特性
確かに、伝達関数の周波数応答特性を実測から求めるといういままでの説明からでは、G3/(1+Go)の周波数応答がどうなるか、考えるのはちょっと難しいな。このあたりで、伝達関数の演算とその周波数応答特性の関係について、もう少し詳しく説明してみようか。 まず周波数応答特性が何かという説明はしなくてもええよな?
前回教えてもらったからいいよ
周波数応答特性を表現する方法として、ボード線図とベクトル軌跡があるけどどちらも本質的には同じことや。私は専らボード線図を使ってきたので、ここでもボード線図に限定して説明するで
分かったよ
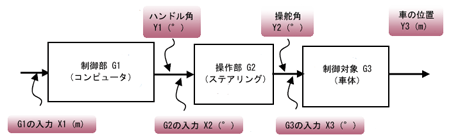
前回、車の自動運転制御システムの開ループシステムGoのブロック線図を示したやろ?
あぁ、あったね。あのボード線図は、リモコンで車を左右に操作して、車の周波数応答特性を計測したんだったね
確かに、実験計測で伝達関数の周波数応答を直接求めてもええけど、それでは大変な場合も多いし、第一、設計段階で試作品が存在していない状態では計測できない
確かにそうだね
実は、各伝達関数の周波数応答特性は、測定対象の物理モデルを構築することで推定することができます。そして開ループシステムGoを構成する各伝達関数Gi(i=1,2,3) の周波数応答特性が分かれば、開ループ伝達関数Goの周波数応答特性を求めることができます。従って、リモコンで車を操作するような大袈裟な装置を作る必要はありません。
車のステアリング操作部G2はハンドルモータ、ステアリングモータなどから構成されています(第3回の図4)が、この物理モデルから操作部G2のボード線図、つまり周波数応答特性は図2のように推定することができます。推定方法については、後に解説する動特性のところで説明します。ここではG2のボード線図は実験計測によって得られたということにします。今回は、制御対象である車の走行特性の伝達関数G3の周波数応答特性の理論的推定方法に限定して説明します。
すべての伝達関数の周波数応答特性も理論的に推定することができるけど、いきなり全部説明しても頭に入らんやろ? だから、今日は車の走行の伝達関数G3の周波数応答特性が、どうやって推定できるか説明するわ
僕をバカにしてるねぇ〜。まぁ、いいけど
そういうワケやないで。理解というものは、同じことを少しずつ、繰り返し、繰り返し学習することで得られるからや。天才は、その回数が少なくて済んだり、一度に多くの量を理解できるってことにおいて普通の人に勝っているだけや。理解の深さには違いはないんや。たぶん……
まあ要は、凡人は繰り返しによって理解しろ! ってことね?
ちょっと違うな。どんな難しいことも、凡人でさえ、繰り返し学習すれば理解できる! ってことや。いわんや、草太ならもう少し努力すれば……何でも分かる!
くすぐったいこというね
で、車の走行特性の伝達関数であるG3の入力は、操舵角度X3(°)で、出力は車体の位置Y3(m)だったな。Y3は直進道路のセンターラインを基準として、センターラインと垂直方向の動きだ。ただし、ここで注意してほしいのは、G3は操舵角度X3に対する車体の横移動を生み出す機能を持ったもの、ということだ。だから、時間経過がなければY3にはなんの変化もない
車が動き始めてから、時間が0からtまで経過すれば、その移動量はこの式だ。この程度の数式は問題ないやろ?
そうだね。単位時間辺りの移動量を積分すれば、現在の横方向位置Y3が分かる
ところで、周波数応答では、入力である操舵角X3を、振幅χ3(°)とする周波数ω(rad/s:ラジアン毎秒)の正弦波で変化させるから、
X3=χ3・sin(ω・t)(°) (15)
だ
うん、うん。するとY3は……(式16)。
sinの中にsinが入っている。この計算はどうするんだろうなぁ
こういう場合の常套(とう)手段を知ってるやろ?
ああ、あれね。非線形を線形化するってやつね。(13)で、X3の振幅χ3(°)が小さいならば、その結果、
sin(π・χ3・sin(ω・t)/180)≒π・χ3・sin(ω・t)/180 (17)
と見なせるだろう。だから、(16)は……
図に書くと、図4のようになるね
あれっ? 出力の波形が上にちょっとずれているね
周波数応答特性は、振幅比と位相差を計測するので、波形のずれは気にしなくていいんや。で、図4から分かるように、Y3の振幅は
(vχ3π)/(180ω)(m)
で、位相遅れは90(°)や
伝達関数G3の振幅比を|G3|、位相差を∠G3と書くことにすると
|G3|=(vχ3π)/(180ω)/χ3=(vπ)/(180ω)(m/°) (19)
∠G3=-90 (°)
ということだね。
あるいは、振幅比をデシベル表示すれば、
20・log(|G3|)=20・log(vπ/(180ω))=20・log(vπ/180)−20・logω (dB) (20)
エクセルを使って、(20)からG3のボード線図を作成すると、図5のようになることは理解できるよな?
ボード線図の横軸は周波数ωの対数表示だから、図5のように、10倍の周波数変化に対して、こう配が−20(dB:デシベル)の直線となるんだ
そして、図2のG2のボード線図を足し合わすとG2・G3のボード線図が得られる
ちょっと待って! G2とG3を足し合わすってどういうこと?
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞




 第3回 図3
第3回 図3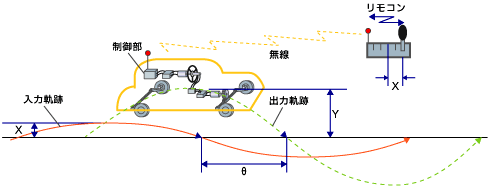 第3回 図9
第3回 図9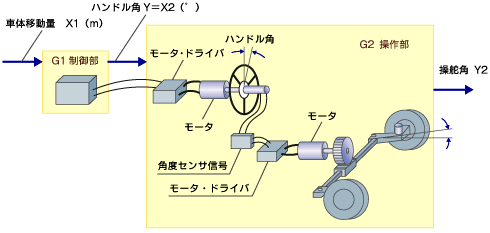 第3回 図4
第3回 図4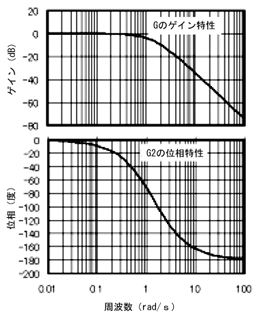 図2 操作部G2のボード線図
図2 操作部G2のボード線図 
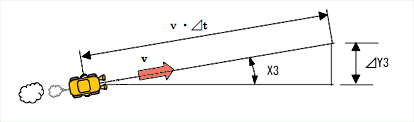 図3 微少時間△t経過後の 車の横方向移動量△Y3
図3 微少時間△t経過後の 車の横方向移動量△Y3
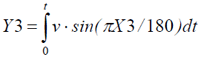
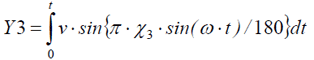
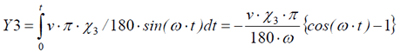
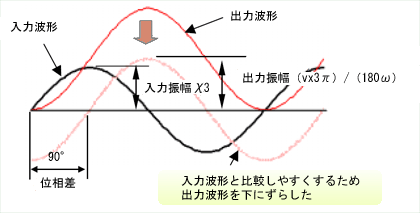 図4 G3の周波数応答出入力波形
図4 G3の周波数応答出入力波形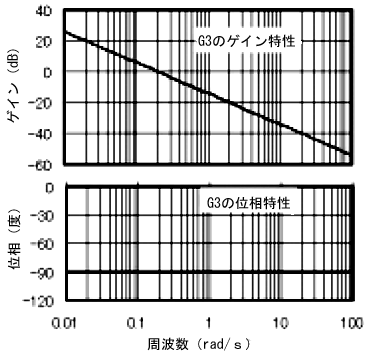 図5 車体の走行特性G3のボ−ド線図
図5 車体の走行特性G3のボ−ド線図





