ダイオードなどの非線形負荷を節点法で解析する:SPICEの仕組みとその活用設計(3)(2/3 ページ)
非線形負荷の直線近似
非線形負荷の場合、電圧・電流特性は一般に曲線になっています。このままでは代数的に解くのは困難ですから図4のように、ある1点の電圧を仮定して、この電圧における曲線の電流変化率を接線コンダクタンスGxとして考えます(Gx=ΔI/ΔV)。
しかし、図4の例から分かるように、負荷をGXだけと考えると、流れる電流はIx=Gx・Vxとなって実際の負荷電流に対して差を生じ、動作点が実際と異なってしまいます。このため補正電流が必要になります。
この補正電流をIeqとすると、式(3)のように非線形負荷の電流を模擬的に表すことができます。
この直線はGXが曲線の接線ですので、仮定した1点の電圧上だけですが非線形負荷と模擬負荷の電圧・電流値を図4のように重ねることができます。
1次線形方程式の解法
負荷線、非線形負荷の模擬負荷、ともに1次線形方程式なので、図5のように、その交点では“AX+B=CX+D”が成立します。これは1次線形方程式ですから、αX+β=0とまとめることができ、この式ならSPICEで動作点を求めることができます。このようにして求めた動作点(=交点)が、もし図4で仮定した電圧と等しければその値が実際の非線形負荷の動作点となります。
また、求めた交点が仮定した電圧値と等しくない場合でも、求まった交点は図6に示すようにV0で仮定した値より確実に真値に近いはずであり、これらを繰り返していけば、V0→V1→V2→…と、ある程度の誤差を有するものの、最終的には許容できる範囲に収まります。
「負荷線と模擬負荷の交点」ということは、交点ではF(X)=G(X)が成立します。この関係を整理すると、
という、冒頭で取り上げたNewton-Raphson法の式に戻ります。
しかし、いきなりf(X)=0という形で表現すると、何を求めようとしているのかが明確でなくなるので、電子回路ではこのように交点(動作点)を考えた方が物理的な意味がよく分かるのです。
ダイオードの特性解析
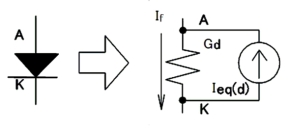
図7に示すダイオードの負荷特性を回路要素行列[G]に組み込むために、最初にダイオードの特性を図4に習ってコンダクタンスと電流源の式で表現します。
Gdは印加電圧Vfにおける接線コンダクタンスですから、式(4)のようにIfをVfで微分して得ます。
これらの関係を図7に示しますが、接線コンダクタンスGdと補正電流Ieq(d)でダイオードの動作を表していることが分かります。そして、図7の特性を実現する等価回路は図8に示す構成になります。
しかし、式(4)、(5)から分かるように、Ieq(d)、GdはVfの関数なのですが、Vfが求まっていないので値を決めることができません。
Newton-Raphson法を使うには初期値は絶対必要ですので、ここでは初回のVf0として一般的な0.7Vを与え*1)、次の計算サイクルより計算結果を代入することとします。
*1)他にも、回路の初期条件から回路方程式を解き、得られた回路状態から素子のオン/オフを決める方法などがありますが、詳しい説明は今回の記事の目的から外れますので、ここではこれ以上触れません。
このように初期値のVf0と式(4)、(5)から初回のIf、Gd、Ieq(d)を計算して回路要素行列[G]を生成し、解として得られた値Vf+1が仮定した値(=Vf)の一定の誤差内になるまで繰り返して近似解を求めます。
このように、使う数式が素子ごとに決まっていて、その関数が微分可能であるならば、上記手順で模擬負荷の等価回路をあらかじめ決めておくことができます。SPICE解析においてライブラリファイルが必要になるのはこのような背景からなのですが、ライブラリについては回を改めて説明します。
Copyright © ITmedia, Inc. All Rights Reserved.
Factory Automationの記事ランキング
- これ板金? ちょっと何言っているかよく…第38回優秀板金製品技能フェア各賞紹介
- 「そのラダープログラム10年後も読めますか」――オムロンが描くAI活用
- AGVか、それともAMRか……無人搬送機導入時の注意点
- 同じ原理は超高速で走る“あれ”にも! ある装置の音
- DMG森精機と東大がMXセンターを設立、森氏は“機上計測”に関心
- 「深夜特急」のイラン
- 物流自動化は「入れて終わり」ではない、本社と現場の分断を越える“キーマン”とは
- ロックウェル「自律型工場」への道筋、5つのステップと7つの技術要素
- 2033年に年間1万人相当の供給体制、第1弾は手足のシンクロ可能な移動ロボ
- 鋳造/鍛造品向け切削加工AIの共同開発合意、アルムと神戸製鋼所
コーナーリンク
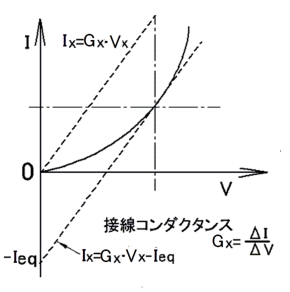 図4 負荷接線と補正電流
図4 負荷接線と補正電流 図5 交点を求める
図5 交点を求める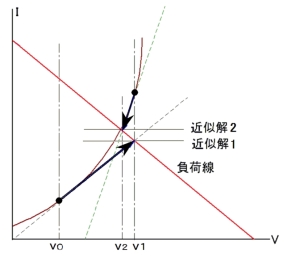
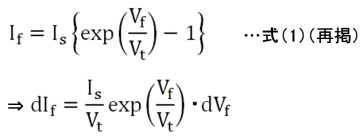
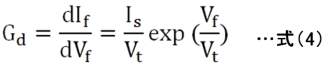
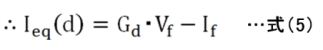
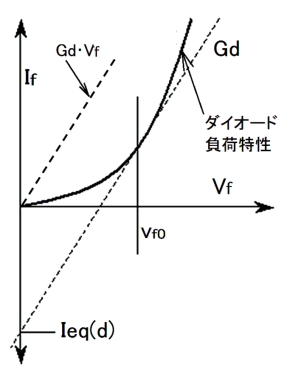 図7 ダイオードの特性例
図7 ダイオードの特性例