フローで考える熱のモデリング(その2) 〜熱コンダクタンスの定義と導出方法〜:1Dモデリングの勘所(32)(1/5 ページ)
「1Dモデリング」に関する連載。連載第32回では「フローで考える熱のモデリング(その2)」と題し、熱コンダクタンスの定義とその導出方法について取り上げる。
熱のモデリングでは、「熱コンダクタンス」の定義方法を正しく理解しておく必要がある。伝熱の3形態、すなわち「熱伝導」「対流熱伝達」「放射伝熱」について、熱コンダクタンスをその導出手順も含めて説明する。対流熱伝達に関しては、流れが関係するため、その理論的側面についてもやや煩雑ではあるが解説する。また、対流熱伝達に関しては、流れの形態によって「強制対流熱伝達」と「自然対流熱伝達」が存在することと、これらを熱コンダクタンスに結び付けるためのいくつかの重要な無次元数について紹介する。
熱コンダクタンス
前回述べたように、熱に関しては式1が成り立つ。
Q[W]は熱量、T[K]は温度である。左辺第1項を変形すると、
となる。G[W/K]は熱コンダクタンスで、その単位から分かるように熱の流れやすさを示す指標である。従って、熱のモデリングおいては、熱コンダクタンスをいかにして定義するかが重要となる。一方で、熱の伝わり方は前回述べたように、その形態(熱伝導、対流熱伝達、放射伝熱)によって異なるため、熱コンダクタンスの定義方法も異なってくる。
熱伝導に関する熱コンダクタンス
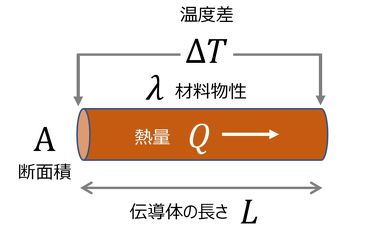
図1に示すように、断面積A[m2]、長さL[m]の熱伝導体(外壁は熱断熱されているとする)に熱量Q[W]が流れていて、その両端の温度差がΔT[K]である場合を考える。
このとき、以下の式3が成り立つ。
G[W/K]が熱伝導に関する熱コンダクタンスで、
で定義される。λ[W/m・K]は熱伝達率で物質により決まる値である。図1の伝導体は円形断面であるが、断面形状は問わない。また、断面が変化する場合には、任意の位置の断面積をA(x)[m2]として、熱伝導の基本式に立ち返って考えると、
となる。
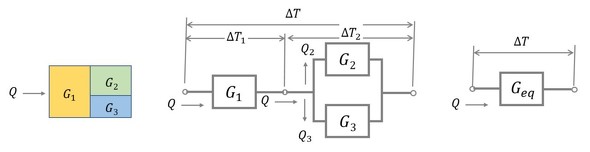
伝熱方向に物質が変化する場合には、図2に示すように等価回路の考え方で、等価な熱コンダクタンスを定義できる。
図2左図のような構成を考え、これを回路表現すると図2中図となる。ここに、
となり、
となる。これより、
となるので、最終的に等価な熱コンダクタンスGeqは、
となる。
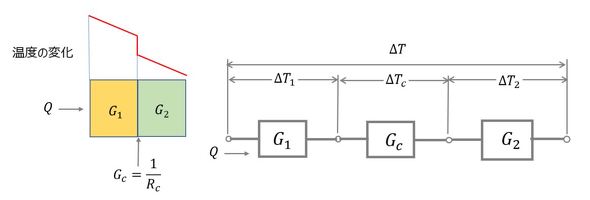
一方、物質と物質が接触している場合に、熱移動が存在すると、物質間には温度差が生じる。このときの物質間の熱抵抗(熱コンダクタンスの逆数)を「接触熱抵抗」という。この場合も同様に、等価な熱コンダクタンスを定義できる。図3に示すように2つの物質が接触している場合には、
となる。ここに、Gcは接触熱抵抗Rcの逆数である。
Copyright © ITmedia, Inc. All Rights Reserved.