フローで考える熱のモデリング（その1） 〜熱の理論と熱回路網解析〜：1Dモデリングの勘所（31）（1/4 ページ）

「1Dモデリング」に関する連載。連載第31回では「フローで考える熱のモデリング（その1）」と題し、フローで考える熱の理論と熱回路網解析について取り上げる。

[大富浩一／日本機械学会 設計研究会，MONOist]

　前回、前々回の流れのモデリングに続き、今回は「フローで考える熱のモデリング（その1）」と題して、フローで考える熱の理論と熱回路網解析について取り上げる。流れと共通する部分も多いが、熱固有の問題もあるので、この辺りを中心に解説する。

⇒連載バックナンバーはこちら

フローで考える熱の方程式

　連載第28回で述べたように、熱に関しては次式が成り立つ。

式1

　Q［W］は熱量、T［K］は温度である。左辺第1項を変形すると、

式2

となる。これから、係数Gが大きいほど熱は流れやすいことが分かる。そこで、G［W/K］を「熱コンダクタンス」と呼ぶことにする。一方、左辺第2項を変形し、積分すると、

式3

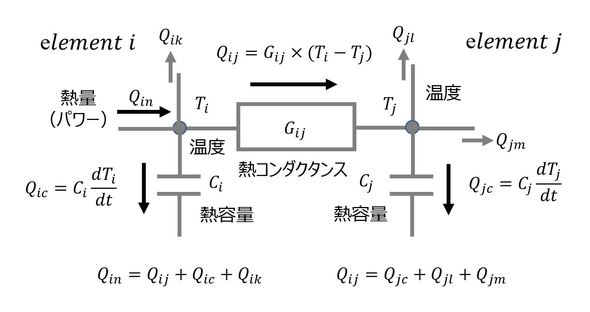
となる。これから、係数Cが大きいほど熱エネルギーが大きい、すなわち熱を多く蓄えられることになる。そこで、C［J/k］を「熱容量」と呼ぶことにする。熱の式を基に、熱に関する構成要素の一部（要素i，j）を抽出して表現すると図1となる。要素iおよび要素jに流入する熱量は流出する熱量に等しい（電流則）ことにより、

式4

が成り立ち、温度と熱量の関係式（電圧則）により、

式5

が成り立つ。要素iおよび要素jから外部への熱の流れがないものとすると、未知数は温度T_i、T_j、流量Q_ic、Q_ij、Q_jcの5つであり、上記の式の数と一致するため解くことができる。実際には、n個の要素で構成されるより複雑な熱系においても同様に解くことが可能だ。

　図1および熱の式を前回、前々回の流れの場合と比較すると、慣性項が存在しないことに気が付く。慣性項は電気、振動の場合にも存在し、熱についてのみ存在しない。これは事実なのでその理由を詮索することにあまり意味はないが、電気の場合は電荷、流れの場合は流体、振動の場合は質量という移動素子があるのに対し、熱の場合は分子の熱振動が伝搬する現象であり、移動素子に起因するものではないためだと思われる。

図1　フローで考える熱［クリックで拡大］