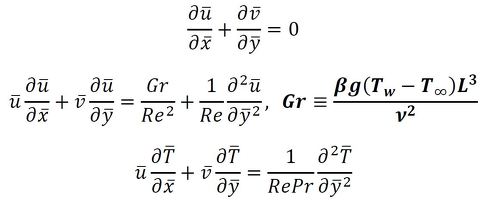連載
フローで考える熱のモデリング(その2) 〜熱コンダクタンスの定義と導出方法〜:1Dモデリングの勘所(32)(3/5 ページ)
「1Dモデリング」に関する連載。連載第32回では「フローで考える熱のモデリング(その2)」と題し、熱コンダクタンスの定義とその導出方法について取り上げる。
自然対流熱伝達
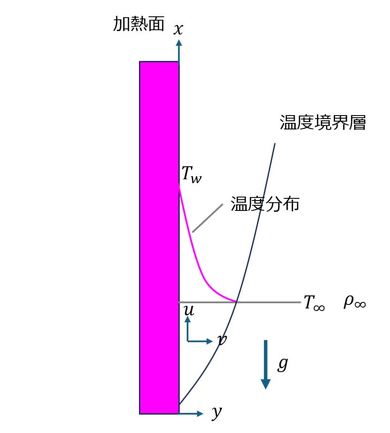
以上、強制対流熱伝達について議論してきた。ここで、最初に戻って自然対流熱伝達について考える。図7に示すように、垂直加熱平板に沿った2次元の定常的な自然対流を考える。
流れは層流で、重力は図の下向き(−x方向)に作用している。自然対流の運動方程式は既に導出した運動方程式で、体積力Fx=−gを考慮すればよい。すなわち、
となる。境界層近似では境界層外の圧力がそのまま境界層内に及び、境界層外では流体の動きはないので、
となる。この式を最初の式に代入すると、
となる。
一方、流体の熱膨張に関しては、次の関係が成り立つ。
βは体膨張係数である。上記の関係を用いて、前々式を表現すると下記となる。
連続の式、エネルギー方程式は同様なので、支配方程式は以下となる。
上述の式を、強制対流熱伝達と同様に無次元化すると以下となる。
Grを「グラスホフ数」と呼び、粘性力に対する浮力の大きさを示す。以上から、
となる。
Copyright © ITmedia, Inc. All Rights Reserved.