乱流シミュレーションを使いこなす:CAE解析とExcelを使いながら冷却系設計を自分でやってみる(13)(1/4 ページ)
CAE解析とExcelを使いながら冷却系の設計を“自分でやってみる/できるようになる”ことを目指す連載。連載第13回は、乱流シミュレーションについて解説する。
お待たせしました。いよいよ乱流シミュレーションです。では、最もよく知られている「k-εモデル」から入りましょう。流体シミュレーションソフトでは乱流モデルを選択する場面がありますが、およそ20種類くらいの中から1つを選びます。第1選択肢はk-εモデルとなります。k-εモデルは粗い要素分割でも、そこそこの計算精度が得られる点が利点です。まずはk-εモデルで計算して様子を見て、必要に応じて目的に合った他の乱流モデルを選択することになります。
k-εモデル
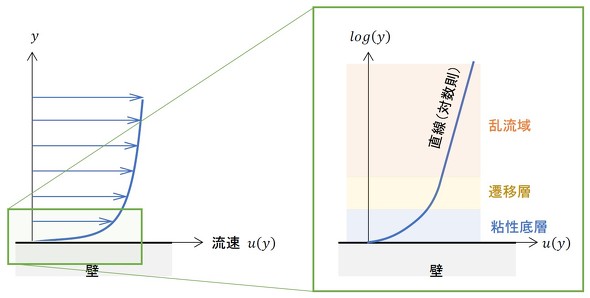
図1に、円管内部の速度分布を再掲します。
層流と乱流では、速度分布が全く異なります。層流の速度分布は「ナビエ・ストークス(Navier-Stokes)式」から導きました。ということは、乱流はナビエ・ストークス式だけでは直接求められていないということになります。乱流の解析では、ナビエ・ストークス式に加えて乱流モデルを導入して計算を行います。乱流モデルの1つにk-εモデルがあります。
図1の壁面近傍の速度に注目します。乱流の場合、速度の変化は急峻(きゅうしゅん)です。動画1は、前回紹介した内容の再掲です。
これを見ると、水道水の流れは乱流ですが、ポビドンヨード液はなかなか流れ落ちてくれません。板の表面近傍では、流れがかなり遅いようです。この領域は「粘性低層」と呼ばれています。
板表面近傍、つまり壁面近傍の速度分布を図2に示します。
図2右図において、縦軸は対数目盛であり、縦軸、横軸ともに無次元数で表しています。ポビドンヨード液がなかなか流れなかったのは、ポビドンヨード液が粘性底層にあったためです。粘性底層は層流であり、速度分布は放物線になります。動画1の水道水が勢いよく流れている領域は、対数グラフ上で直線となり、「対数則」という経験則が適用できる領域です。
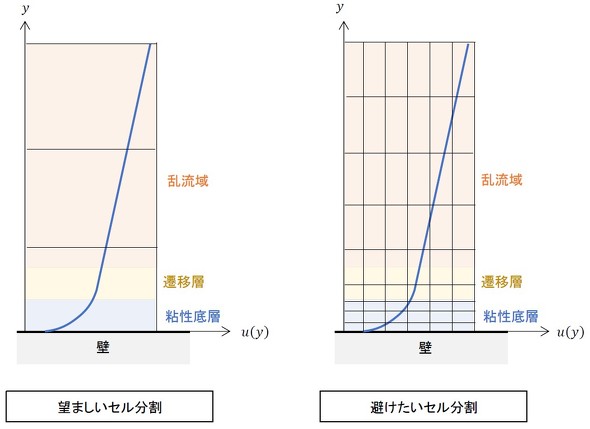
以前お届けした連載「CAEを正しく使い疲労強度計算と有機的につなげる」では、弾性解析は要素分割を細かくすると、弾性力学による厳密解に近づくと述べました。しかし、k-εモデルを使う場合は、セル分割を細かくしてはいけません。壁に接するコントロールボリューム(ここでは直方体として描いていますが、通常は多面体です)は特別な扱いであり、その中に粘性底層、遷移層、乱流域の一部が含まれるように設計されています。いわば「コミコミ」です。このような速度分布の取り扱いを「壁関数」と呼びます。コミコミであるため、壁に接するセルは、粘性底層と遷移層を含められる程度の大きさにする必要があります。図3に、k-εモデルを使う場合のセル分割の考え方を示します。
セル分割が適切かどうかを判断するための指針として、「Y+(Yplus)」というパラメーターがあります。文献によってさまざまな表現がありますが、例えば次の式1で表される無次元量です。
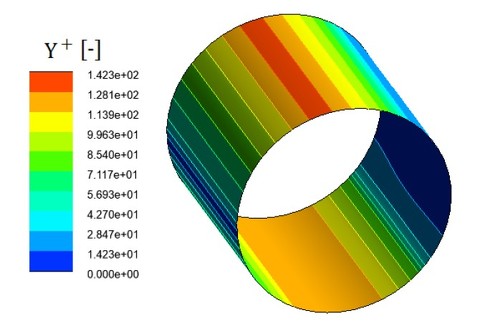
Lをコントロールボリュームサイズと書きましたが、プログラム内部を確認したわけではないため、少し自信がありません。k-εモデルを使用する場合、Y+は100[-]前後となるようにセル分割を行います。なお、100[-]前後という値は一般的な目安であり、ソフトによってはマニュアルに記載されている推奨値が異なることもあります。図4に、Y+の表示例を示します。位置は壁面で、コンター図によって表示しています。
壁関数を導入したおかげで、k-εモデルではセル分割を粗く設定できるため、計算時間を大幅に短縮できます。一方、これから述べる他の乱流モデルでは、粘性底層と遷移層もセル分割する必要があります。この場合、Y+は例えば2[-]以下に設定しなければならず、セル数は数十倍に増加し、計算時間も大幅に伸びます。そういう理由から、第1選択肢はk-εモデルとなります。ちなみに、筆者は「RNG k-εモデル」をよく使います。
注意してほしい点があります。k-εモデルを使用しない場合は、セル分割を図3右図のように行ってください。
Copyright © ITmedia, Inc. All Rights Reserved.