乱流シミュレーションを使いこなす：CAE解析とExcelを使いながら冷却系設計を自分でやってみる（13）（2/4 ページ）

CAE解析とExcelを使いながら冷却系の設計を“自分でやってみる／できるようになる”ことを目指す連載。連載第13回は、乱流シミュレーションについて解説する。

[高橋良一／ＲＴデザインラボ 代表，MONOist]

シミュレーションでは渦はどうなっているのだろうか

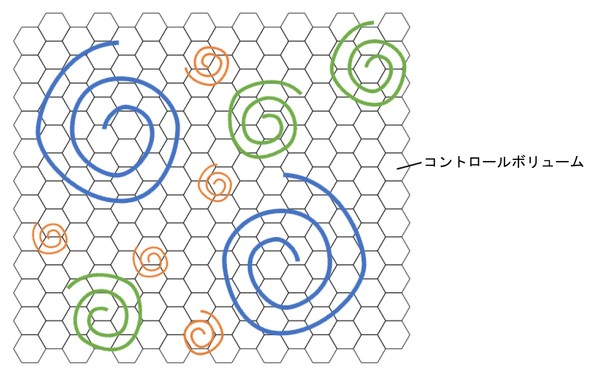
　シミュレーションで渦はどのように扱われているのでしょうか。図5に、コントロールボリュームと渦の関係を示します。

図5　コントロールボリュームと渦［クリックで拡大］

　分割後のセルを四面体と仮定し、コントロールボリュームを多面体で表現しています。コントロールボリュームは1次要素であるため、その内部では速度は一様と見なされます。つまり、渦を表現するには、少なくともこの図の場合、7個のコントロールボリュームが必要となります。図5の青色の渦と緑色の渦は解像できますが、オレンジ色の渦は解像できません。

　ここからは、流体シミュレーションソフトが解像できない渦をどのように扱っているかを説明します。ここで紹介する手法は、「ラージエディシミュレーション（LES：Large Eddy Simulation）」と呼ばれる方法です。解像できない渦は、流体の属性の一種として取り扱われます。例えば、塩水と真水が混ざり合うシミュレーションでは、それぞれのコントロールボリュームが塩分濃度というパラメーターを持ち、その変化を輸送方程式に従って計算します。LESにおける渦は塩分濃度と全く同じ扱いではありませんが、渦の強さや度合いをパラメーターとして取り扱い、計算します。一方、解像できる渦については、そのまま計算します。

　LESでは、見たい渦のサイズを自分で決め、それに応じてセル分割を行う必要があります。見たい渦が小さい場合、セル分割も細かくなります。また、Y⁺の制約も2［-］以下に設定しなければなりません。このため、計算時間が非常に長くなり、解析は過渡応答解析に限定され、定常解は得られません。他の手法で定常解を求めた上で、それを初期値としてLESで過渡応答解析を行う必要があります。

　一方、k-εモデルで解像できる渦は1個か2個程度です。さらに、流速が時間軸に対して平均化されるため、下流へ移動するような渦は解像できません。解像できるのは、移動しない大きな渦に限られます。k-εモデルのような手法は、「レイノルズ平均モデル（RANS：Reynolds Averaged Numerical Simulation）」と呼ばれます。シミュレーション手法については、後ほど一覧表を作成しますね。

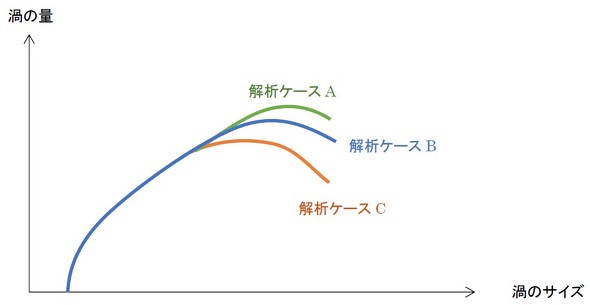
　では、乱流という現象を完全に把握したい場合、どれだけ細かなセル分割が必要なのでしょうか。渦は、無限に小さなものまで分布しているのでしょうか。図6に渦の分布を示します。解析ケースA、解析ケースB、解析ケースCは、形状や流速が異なる解析ケースです。当然、渦の分布も異なりますが、小さな渦の分布は同じになるといわれています。

図6　渦の分布［クリックで拡大］

　そして、渦の小ささには下限があります。ニュートン流体の定義によれば、せん断応力は速度勾配（速度差／距離）に比例します。渦の上下では速度の方向が反対のため、分子（速度差）はゼロにはなりません。一方、分母（距離）は極端に小さくなり、粘性の影響が顕著になります。その結果、渦のエネルギーが熱に変換され、渦が消失すると解釈されます。

　渦の小ささに下限があるとすれば、そのサイズまでセル分割を細かく行えば、LES手法でモデル化していた小さな渦を考慮する必要がなくなります。つまり、ナビエ・ストークス方程式を直接解くプログラムだけで解析が可能となります。これはすなわち、層流解析です。このような手法を「DNS（Direct Numerical Simulation）」といいます。

　DNSによって、層流から乱流へと移り変わる現象を計算した論文を読んだことがあります。しかしながら、下限の渦のサイズは非常に小さく、必要となるコントロールボリューム数は軽く1兆個を超え、時間ステップも極めて細かく設定する必要があります。あるソフトの解説書には、現在のコンピュータ性能では実行は困難であり、将来コンピュータが発達しても実現は難しいかもしれないと記載されていたのを覚えています。

乱流シミュレーションまとめ

　これまでに紹介してきた乱流シミュレーション手法について、表1にまとめておきます。

	RANS レイノルズ平均モデル		LES ラージエディシミュレーション	DNS
渦の解像	1個程度		コントロールポリュームの細かさで決まる	全て解像
解像できない渦の処理	乱流粘性係数などで表現		モデル化	−
乱流モデル	k-ε	k-ω、SST	Smagorinsky、WALEなど	層流モデルとなる
Y+推奨値	100［-］前後	2［-］以下	2［-］以下	−
計算時間	短い	長い	かなり長い	たぶん終わらない
定常解析	可	可	不可	原理的に不可
表1　乱流シミュレーション手法のまとめ

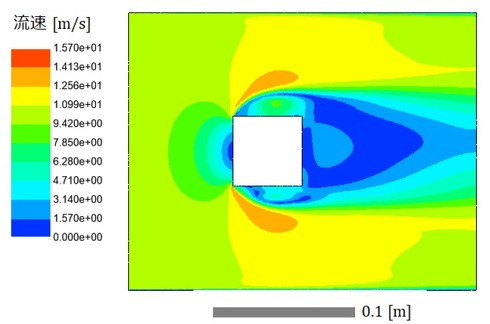
　図7に、RANSによる解析例を示します。乱流モデルは「SST（Shear Stress Transport）」で、渦はおおよそ4個程度です。

図7　RANSによる解析例（乱流モデル：SST）［クリックで拡大］

　図8には、LESによる解析例を示します。乱流モデルは「Smagorinsky」で、セル分割に応じて渦の数が決まります。より小さな渦を再現するには、セル分割と時間刻み幅をさらに小さくする必要がありますが、ソフトウェアの利用費で原稿料がぶっ飛びますので、今回はここまでとします。

図8　LESによる解析（乱流モデル：Smagorinsky）［クリックで拡大］

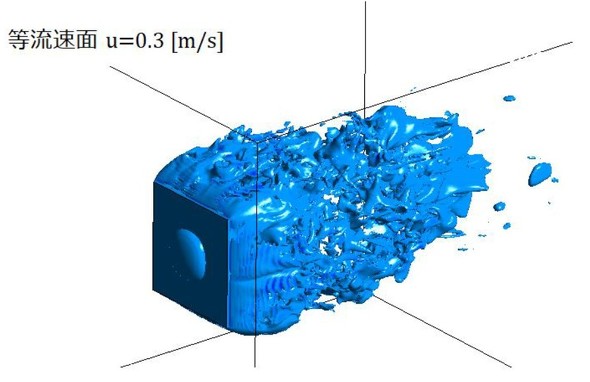
　LES解析において、流速が等しい領域を面としたものを図9に示します。3次元的な渦の生成が確認できます。

図9　LES解析において、流速が等しい領域を面としたもの（乱流モデル：Smagorinsky）［クリックで拡大］