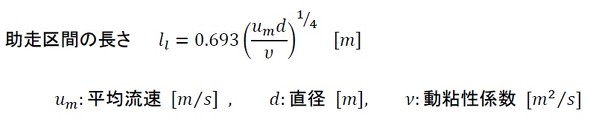乱流シミュレーションを使いこなす:CAE解析とExcelを使いながら冷却系設計を自分でやってみる(13)(3/4 ページ)
CAE解析とExcelを使いながら冷却系の設計を“自分でやってみる/できるようになる”ことを目指す連載。連載第13回は、乱流シミュレーションについて解説する。
円管乱流のシミュレーション
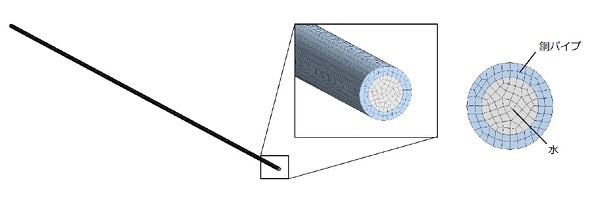
今回は、直径10[mm]の円管内の流れを計算しました。図10にセル分割図を示します。水の部分のセル分割数は8分割と、少なめに設定しています。Y+の制約を考慮すると、さらに粗いセル分割が必要となりますが、それ以上の粗さには筆者として抵抗があったため、このような分割としました。乱流モデルには、RNG k-εを選択しました。
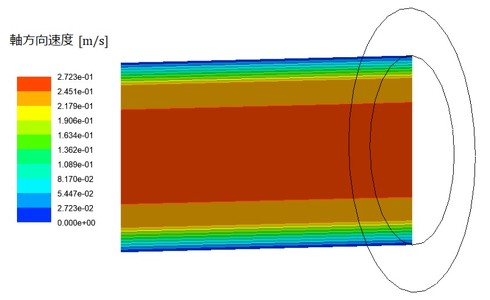
図11に出口近傍の速度ベクトルを、図12に軸方向の速度分布を示します。
図13に圧力分布を示します。
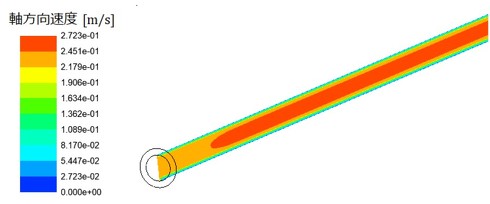
入り口近傍の速度分布を調べましょう。図14に示します。
入り口の境界条件では、速度を入り口断面で一様としていました。これは、大きなタンクに細い管をつないだような状態を想定したもので、入り口近傍の一様流れが7分の1べき乗則に従った分布へと落ち着くまでの区間が存在します。この区間を「助走区間」と呼びます。助走区間の長さは、式2によって求めることができます(参考文献[1])。数値を代入すると、49[mm]となりました。直径が10[mm]なので、図14を見た印象としては、良い線いっているようです。
参考文献:
- [1]日本機械学会|機械工学便覧 A5 流体工学(1992)
紙と鉛筆による計算とシミュレーション結果との比較
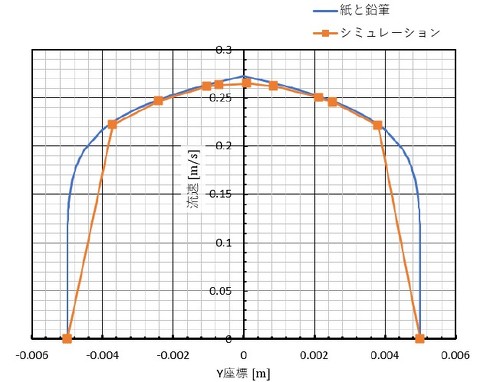
図15に軸方向の流速を示します。
紙と鉛筆による流速は、前回の式3を用いて計算したものです。この計算結果とシミュレーション結果は、よい一致を示しました。シミュレーションのプロットを見ると、壁面に接するコントロールボリュームには粘性底層と遷移層が含まれているようです。
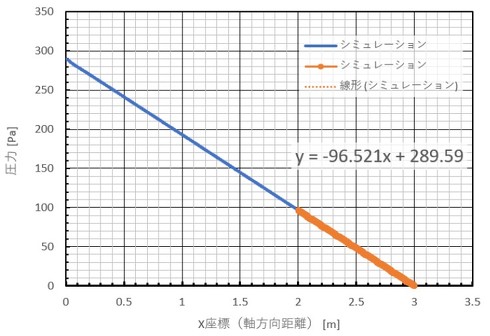
図16に圧力分布を示します。助走区間はありますが、全体としてはほぼ直線的な分布となりました。図中のオレンジ色のグラフの傾きが圧力勾配に相当し、グラフから求めた値は−96.5[Pa/m]となりました。
紙と鉛筆による圧力勾配は、前回の式8から求めることができ、式3となります。数値を代入すると−113.9[Pa/m]となり、圧力損失についてもよい一致が得られました。
以上が、乱流シミュレーションの一例です。
Copyright © ITmedia, Inc. All Rights Reserved.