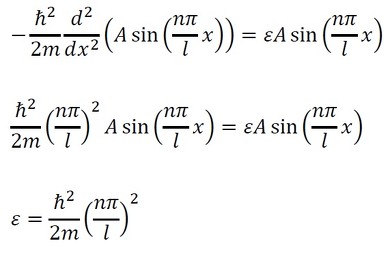時々刻々と変化する温度分布：CAE解析とExcelを使いながら冷却系設計を自分でやってみる（8）（6/6 ページ）

CAE解析とExcelを使いながら冷却系の設計を“自分でやってみる／できるようになる”ことを目指す連載。連載第8回は、非定常熱伝導問題に取り組む。

[高橋良一／ＲＴデザインラボ 代表，MONOist]

箱に閉じ込められた粒子の挙動

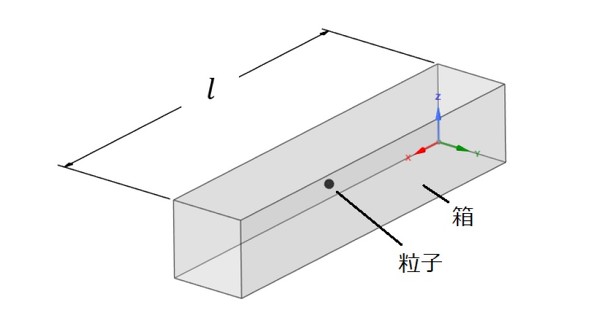
　それでは、式46を解いて、図18のような箱の中にある粒子の挙動を調べてみましょう。粒子はパチンコ玉ではなく、気体分子のような粒子だとお考えください。ポテンシャルエネルギーは箱の中でゼロ、そして粒子が箱の外に出ることはできないため、箱の外ではポテンシャルは無限大です。

図18　箱の中の粒子［クリックで拡大］

　境界条件を考えます。波動関数φ（x）の絶対値の二乗が、粒子がxの位置で見つかる確率密度でした。箱の外では粒子は見つからないため、連続性から壁面でも見つかりません。従って、以下の境界条件が成立します。

式q7

　上式の境界条件と、式q6は2階微分して同じになる関数なので、式q6の解の1つは次式ですね。

式q8

　次式も解ですね。

式q9

　上式に式q6を代入して、εを求めます。

式q10

　εは複素数ではなく実数になりました。

エネルギーの飛び飛びさ加減を見積ってみよう

　式q1から、εは粒子のエネルギーとなります。また式q10から、エネルギーは飛び飛びの値しか持ち得ないことが分かります。

　では、「飛び飛びさ加減」を調べてみましょう。最も低いエネルギー状態（n＝1）と、次のエネルギー状態（n＝2）の差を計算します。

式q11

　飛び飛びさ加減が大きければ大きいほど、量子現象は観測しやすくなります。パチンコ玉の質量を電子の質量で割ると、およそ10の28乗になります。式q11の分母には質量が含まれているため、パチンコ玉では飛び飛びさ加減が電子の10の28乗分の1となり、量子現象が観測しにくくなります。さらに、式q11の分母には箱のサイズ（l）も含まれており、同様のことがいえます。従って、量子現象を観測するには、粒子をミクロな箱に閉じ込める必要があります。

　図17のスリット実験に話を戻しましょう。レーザー光線を用いた場合、干渉縞のピッチは波長に比例した長さになります。今度はたくさんの電子が飛んでいます。

　量子力学においても「運動量」と呼ばれる量が存在しますが、古典力学の運動量は粒子質量と速度との積ですが、量子力学では粒子質量は同じですが速度は粒子の速度のズバリの値と少し違う考え方の量です。そして、運動量は式q5では微分演算子で、観測される運動量は質量と粒子速度のズバリの値との積とは少し意味が異なります。でも、古典力学の運動量と量子力学の運動量は同じ単位を持ちます。つまり、運動量と質量は比例関係にあります。

　式q9のように、波動関数の値は座標が変化するとある周期をもって変化し、その周期性から波長を定義できます。そして、この波長は運動量に反比例するとのことです。古典力学と量子力学の運動量では、速度の扱いが異なる一方で、質量はそのまま粒子の質量が使われます。

　パチンコ玉の質量は、電子の質量に比べて約10の28乗倍大きいため、運動量もそれくらいのオーダーの違いがあるでしょう。よって、パチンコ玉の波長もそれくらいの比で短いことになります。

　レーザー光線の場合、干渉縞のピッチは波長に比例すると説明しました。では、スクリーン上の粒子が作る干渉縞のピッチも波動関数の波長に比例するとしたらどうでしょう。このとき、パチンコ玉が作る干渉縞のピッチは、電子が作るピッチの10の28乗分の1のオーダーとなります。これは測定しようにも、容易に測定できる量ではありません。パチンコ玉のスリット実験は失敗に終わるのではないかと考えています。

　次に、図17右図に示すように、電子がどちらのスリットを通過したかをセンサーなどで観測すると、干渉縞がなくなるという現象について考えてみます。この現象には、筆者では説明できない方程式があり、その境界条件は、

・センサーなし：
　電子銃での存在確率は1［-］、スクリーン上の存在確率は1［-］

・センサーあり：
　片方のスリットでの存在確率は1［-］、スクリーン上の存在確率は1［-］

となります。筆者としては「境界条件が違うのだから結果も違うよね」と考えています。

　以上が、現時点における筆者の解釈です。これ以上深入りすると、ボロが出てしまいそうなのでやめておきます。やはり、量子力学について書こうとすると、筆者の知識がスキマだらけだということを再認識しますね。実は、図17のきれいな画像が1980年代まで撮影できなかったのは、電子のエネルギーをなかなか均一にできなかったからだそうです。

　これまでは熱伝達率を定数として扱ってきましたが、次回から熱伝達率の求め方について解説していきます。……ですがその前に、流体解析のお話から始めたいと思います。　（次回へ続く）

参考文献：

• ［1］清水明｜新版 量子論の基礎｜サイエンス社（2023）

⇒「連載バックナンバー」はこちら

Profile

高橋 良一（たかはし りょういち）
ＲＴデザインラボ 代表

1961年生まれ。技術士（機械部門）、計算力学技術者 上級アナリスト、米MIT Francis Bitter Magnet Laboratory 元研究員。

構造・熱流体系のCAE専門家と機械設計者の両面を持つエンジニア。約40年間、大手電機メーカーにて医用画像診断装置（MRI装置）の電磁振動・騒音の解析、測定、低減設計、二次電池製造ラインの静音化、液晶パネル製造装置の設計、CTスキャナー用X線発生管の設計、超音波溶接機の振動解析と疲労寿命予測、超電導磁石の電磁振動に対する疲労強度評価、メカトロニクス機器の数値シミュレーションの実用化などに従事。現在ＲＴデザインラボにて、受託CAE解析、設計者解析の導入コンサルティングを手掛けている。⇒ ＲＴデザインラボ