連載「CAEを正しく使い疲労強度計算と有機的につなげる」の内容と有限要素法：CAEを正しく使い疲労強度計算と有機的につなげる（2）（1/3 ページ）

金属疲労を起こした際にかかる対策コストは膨大なものになる。連載「CAEを正しく使い疲労強度計算と有機的につなげる」では、CAEを正しく使いこなし、その解析結果から疲労破壊の有無を予測するアプローチを解説する。連載第2回では本連載の「あらすじ」と「有限要素法」について取り上げる。

[高橋良一／ＲＴデザインラボ 代表，MONOist]

　連載第1回では、読者の皆さんを不安にさせてしまいました。連載第2回以降はこの不安を1つずつ取り除いていきます。ちなみに、連載第1回の記事中に有名アニメの題名を少し変えた見出しが8カ所ありました。お気付きになったでしょうか？

　今回は連載「CAEを正しく使い疲労強度計算と有機的につなげる」で取り上げる内容（あらすじ）を紹介するところから始めたいと思います。

⇒「連載バックナンバー」はこちら

本連載のあらすじ

　連載第1回で読者の皆さんを不安にさせてどう始末を付けるのでしょうか。本連載では、以下の内容を取り上げる予定です。これらのほとんどは、論文や書物を読んで筆者なりに解釈した内容となります。筆者の持論を展開するのは最小限ですので、どうぞご安心ください。

• 有限要素法の最小限の説明
• CAEソフトが出力する応力値を真値に近づける考え方 1次要素と2次要素
• おかしな応力値の回避方法 応力特異点
• 金属疲労の発生有無の予測
• 安全率の考え方の新旧
• 溶接部の疲労破断の予測
• 接触要素の必要性
• ボルトの疲労破断の予測
• ボルトの疲労破断の予測に必要とするCAEソフトの仕様

　前回、機械の部品が疲労破断した場合と、1回の荷重で破断した場合とでは、その後の始末に要する工数と費用は1桁程度違う旨を説明した通り、“CAEを正しく使って疲労強度計算をする内容”が本連載の幹となります。そのためには、CAEソフトが出力する応力値を正しい値に近づけるテクニックが必要です。この「テクニック」という言葉から何か裏技的な印象を抱くかもしれませんが、裏技ではなく“正しく使う方法”を説明するだけです。これを知ればCAEソフトに仕掛けられたトラップを回避できると思います。

　CAEを正しく使って応力集中部の応力を正しく求められたら、この結果を金属疲労発生の有無の予測に使うのですが、応力集中部の応力をそのまま使うと過剰品質の設計になります。応力集中度合いを表す係数が応力集中係数αで、応力集中によって疲労強度が低下する度合いが切欠係数βでした。βは実験でしか求まりません。αとβが一致していたら都合がいいのですが、そうではないことを説明し、金属疲労発生の有無の予測方法を紹介します。

　切欠係数βの後に、安全率を説明します。材料の引張強さを荷重作用時応力で割算した値を安全率として、8［-］くらいあったらよしとしている読者もおられると思います。この過程では、応力集中の影響と平均応力の影響が入り込んでいません。切欠係数βを考慮した疲労強度計算の考え方（参考文献［1］）を説明します。

　溶接部の疲労強度データは「公称応力」で整理されています。公称応力とは、荷重を断面積で割った値や、はり理論で求めた曲げ応力のことです。CAEソフトは応力集中部の応力計算は得意ですが、公称応力を求めるのは苦手です。CAEソフトと表計算ソフト「Excel」を使って、公称応力を求めて溶接部の疲労破断の有無を予測しましょう。

　接触要素を特出ししたことには理由があります。連載第1回のフレーム構造物のように壊れるとしたら結合部です。フレームが「ポキッ」と折れたことは聞いたことがありません。結合部品ないしはその近傍、そしてボルトが壊れます。結合部の応力を求めるには接触要素を使う必要があります。接触要素を使った結合部の検討事例を紹介します。

　以前の連載でボルトの話をしましたが、ボルト特有の疲労破断についてより詳しく説明します。疲労に関しては、以前の連載内容の全面改訂となります。ねじ締結部の解説はボルト1本の疲労強度に関する内容です。では、ボルト10本使いのときの許容される繰り返し荷重はボルト1本の場合の10倍でしょうか。ボルト10本使いのときは10倍から「ドカーン」と小さくなることと、複数本使いのときの許容荷重の考え方について解説します。

　多くのCAEソフトは、ボルト締結部のモデリング機能が付属しています。しかし、それらはボルトで固定されている部品側の強度検討のためのもので、ボルトそのものの強度検討のためのものではないように思えます。ボルトの強度検討のためにはボルトをモデリングし、初期締結力をシミュレーションの中で再現して、応力振幅を求める必要があります。このために要求されるCAEソフトの仕様を説明します。CAEソフトないしは3D CADの選定の参考となれば幸いです。説明する順序は前後しますがお付き合いください。

参考文献：

• ［1］日本機械学会｜金属材料 疲労強度の設計資料 I（1991）

CAEソフトが出力する応力値を真値に近づけよう

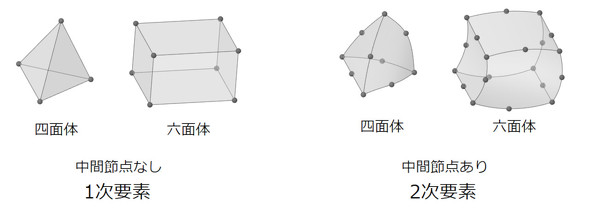
　CAEソフトが出力する応力値を真値に近づけるためには、「1次要素」と「2次要素」の違いを知る必要があります。図1に1次要素と2次要素を示します。

図1　1次要素と2次要素［クリックで拡大］

　1次要素は“中間節点なし要素”、2次要素は“中間節点あり要素”としても区別できます。節点の数で区別して、4節点四面体要素、6節点四面体要素、10節点四面体要素、20節点四面体要素とも呼ばれます。四面体要素の他に、三角柱要素やピラミッド型要素などがあります。ピラミッド型要素は四面体要素と六面体要素を節点結合するときに必須となります。

　2次要素の方が断然計算精度が良いことを説明したいのですが、形状関数をいきなり出しても、すとんと腹落ちしないように思います。少し遠回りになりますが「有限要素法」について説明しようと思います。いくつか文献（参考文献［2］［3］［4］）がありますが、どれも100ページ以上あるので、A4用紙10枚ちょっとで収まる最小限の有限要素法ソフトが作れるくらいの情報量の説明を試みてみましょう。ちなみに、連載の構想段階では、いまさら有限要素法のウンチクを傾けるのはどうかと思っていたのですが、A4用紙10枚くらいなので取り上げることにしました。

参考文献：

• ［2］戸川｜有限要素法概論｜培風館（S56）
• ［3］三好｜有限要素法入門｜培風館（S53）
• ［4］O.C.ツィエンキーヴィッツ｜基礎工学におけるマトリックス有限要素法｜吉識、山田 監訳（S50）

有限要素法入門

　ここでは、以下の順序で説明します。

1. 要素剛性マトリクスの簡単な説明
2. 全体剛性マトリクス
3. 連立方程式の解法、変位の計算
4. 変位からひずみの計算
5. ひずみからと応力の計算
6. 要素剛性マトリクスの導出

　ちなみに、1次要素と2次要素の計算精度の違いを理解するには、「4．変位からひずみの計算」と「5．ひずみからと応力の計算」を押さえておく必要があります。