時々刻々と変化する温度分布：CAE解析とExcelを使いながら冷却系設計を自分でやってみる（8）（5/6 ページ）
CAE解析とExcelを使いながら冷却系の設計を“自分でやってみる／できるようになる”ことを目指す連載。連載第8回は、非定常熱伝導問題に取り組む。
CAE解析との比較（2）
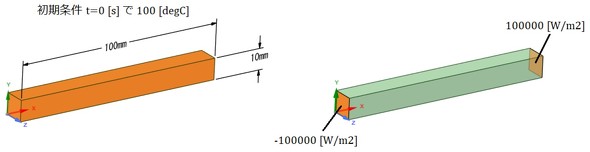
それでは、CAE解析を行いましょう。表1［再掲］に材料定数を、図14にCAE解析の境界条件を示します。
| 密度 ρ | kg/m3 | 7850 |
|---|---|---|
| 熱伝導率 λ | W/m.K | 60.5 |
| 定圧比熱 Cp | J/kg.K | 434 |
| 温度伝導率 a | m2/s | 1.78×10-5 |
| 表1 材料定数［再掲］ | ||
図15に、時刻100［s］での温度分布を示します。
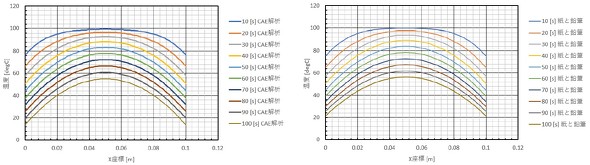
図16に、CAE解析の結果と式29による計算結果を示します。そこそこ一致しましたね。過渡応答解析は時間変化を数値積分によって求めているため、時間の経過とともに少しずれていきました。
2階微分して同じになる関数
2階微分しても同じ形になる関数といえば、sin（x）とcos（x）、そしてexでした。これを使ってもう1つ微分方程式を解いてみましょう。
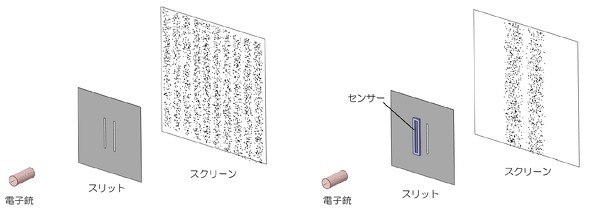
その前に、皆さんは図17に示したスリット実験をご存じでしょうか。2つのスリットを通過した電子のスクリーン上の位置を観測すると、干渉縞のような分布が現れるという実験です。きれいな干渉縞の撮影ができたのは1980年代と比較的最近のことです。筆者の使用していた物理の教科書はそれ以前に書かれたものですが、干渉縞が生じると記されていました。そして、図17右図に示すように電子がどちらのスリットを通ったかをセンサーなどで観測すると、干渉縞がなくなるという内容です。
量子現象は“ミクロの世界の話”といわれていますが、パチンコ玉でも干渉縞が現れるのでしょうか。例えば、部屋を真っ暗にし、パチンコ玉がどちらのスリットを通過したか分からないように工夫し、同時に部屋の壁には粘土を塗り付けておきます。また、多くの量子コンピュータと同様に、屋全体を極低温に冷却したと仮定しましょう。この状態でパチンコ玉を全部飛ばし、壁の粘土に付いた衝突痕の分布を観測します。
量子現象はフォトン、電子、原子核、原子、分子などで観測されます。粒子の大きさには幅があり、その上限は筆者の知る限りありません。もしかしたら、粘土のへこみの分布に縞ができるかもしれません。パチンコ玉ではなく「丸焼き用チキンを飛ばしたら」と書かれた文献もありますが、ここではパチンコ玉で干渉縞が観測できるかを考えてみましょう。
波動方程式を作ろう
ここでの波動方程式は、ギターの弦の振動ではなく「シュレーディンガー方程式」です。次式は古典力学のエネルギー保存則でしたね。
ポテンシャルエネルギーV（x）については、例えば地球上ならmgx、水素原子核の電子なら− e2／4πε0r（※4）です。
運動量pは次式でした。
式43をvイコール（＝）の形にして式q2に代入します。
ここで以下の置き換えを行います。
運動量の2乗だったところを、d／dx（※5）を2回作用させて（2階微分にして）、式q4の両辺の右側に波動関数φ（x）を挿入します。
時間に依存しないシュレーディンガー方程式になりました。運動量を数値を持つパラメーターに置き換えるのではなく、微分演算子に置き換えています。「こんなのありか……」と思うのですが、このような作業を「正準量子化」と呼び、“量子論を一義的に決定する能力はないが、便利である”とされています。
式q6は、ある関数φ（x）に演算子を掛けた結果が、関数φ（x）に数値εを掛けたものと等しくなる形をしており、固有値問題として解釈できます。
Copyright © ITmedia, Inc. All Rights Reserved.