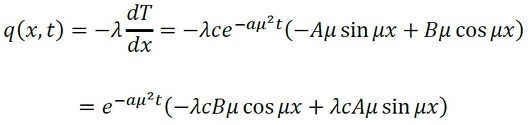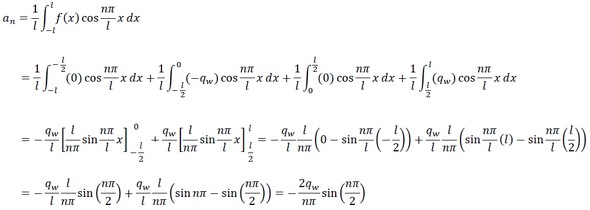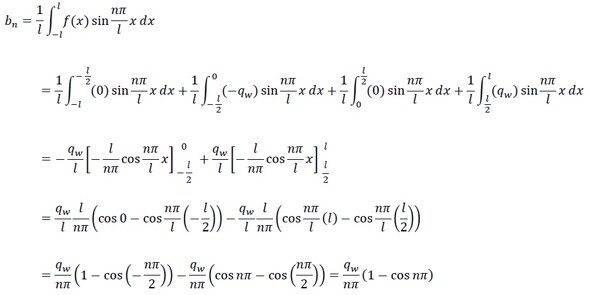時々刻々と変化する温度分布：CAE解析とExcelを使いながら冷却系設計を自分でやってみる（8）（4/6 ページ）
CAE解析とExcelを使いながら冷却系の設計を“自分でやってみる／できるようになる”ことを目指す連載。連載第8回は、非定常熱伝導問題に取り組む。
CAE解析との比較（1）
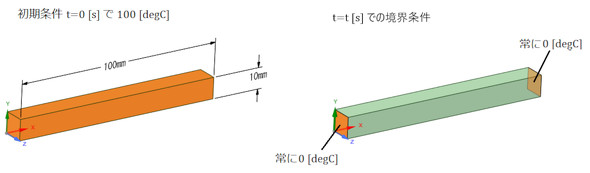
では、CAE解析を行いましょう。表1に材料定数を、図6にCAE解析の境界条件を示します。
| 密度 ρ | kg/m3 | 7850 |
|---|---|---|
| 熱伝導率 λ | W/m.K | 60.5 |
| 定圧比熱 Cp | J/kg.K | 434 |
| 温度伝導率 a | m2/s | 1.78×10-5 |
| 表1 材料定数 | ||
図7に時刻100［s］での温度分布を示します。
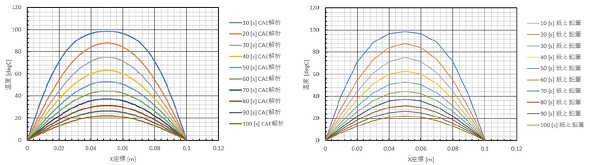
図8に、CAE解析結果と式29による計算結果を示します。一致しましたね。筆者の少し自信のない紙と鉛筆による計算結果をシミュレーションで確認したようなものです。普通はCAE解析結果に対して「桁あってますか検算」（連載「CAEを正しく使い疲労強度計算と有機的につなげる」の第6回）をするために紙と鉛筆による計算結果を使うのですが、今回はこの反対ですね。
このように、温度を境界条件とするものを「ディレクレ（Dirichlet）境界条件」といいます。一方、温度の1階微分、この場合、熱流束を境界条件とするものを「ノイマン（Neumann）境界条件」と呼びます。
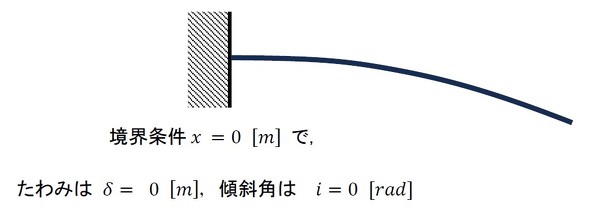
図9に示した片持ちはりのたわみ計算では、x＝0［m］におけるたわみをゼロとするのがディレクレ境界条件、x＝0［m］における傾斜をゼロとするのがノイマン境界条件となります。
熱い棒の両端の熱流束を一定にした場合
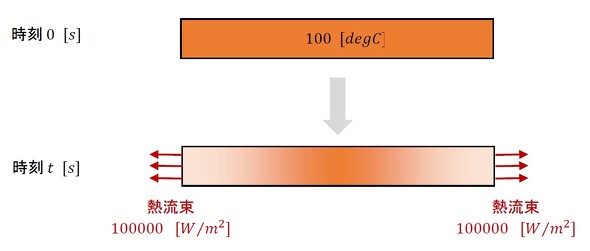
今度はノイマン境界条件の例を述べます。図10に示すように、100［degC］に熱せられた棒の両端の熱流束を一定にした問題です。
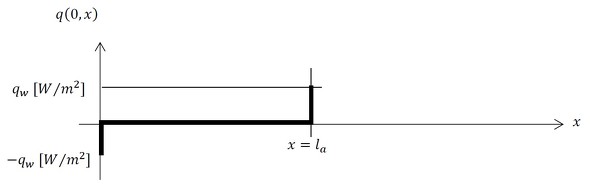
境界条件をグラフにすると図11のようになります。
フーリエ級数を適用するために、ここでひと工夫を加えます。図11を拡張して図12のようにします。こうすることで、この関数は周期関数として扱うことができ、フーリエ級数によって表現可能になります。なお、ここでは2la＝lとなるように長さを操作しています。
方程式、式5の解は次式でした（式30）。
フーリエの法則から熱流束は式31となります。
線形微分方程式に複数の解があったとしたら、それらの和も解となるため、次式が成立します（式32）。
t＝0［s］の熱流束は式33となります。
図12は周期2lの周期関数なので、次のフーリエ級数で表すことができます。a0＝0です。
式16と式33はそっくりです。以下の対応関係を作りましょう。
式34を使うと、以下の対応関係があることになります。
式16のanとbnを求めれば、答えが得られそうです。早速フーリエ級数を計算しましょう。まずは式17です。
次は式18です。
式33に式36と式37を代入します。
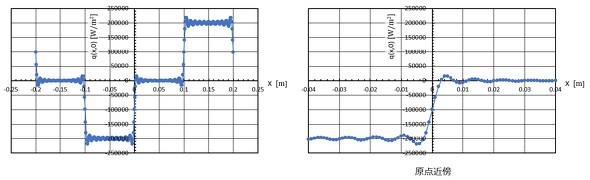
式38を計算しましょう。図13に示します。qw＝200000［W/m2］とし、n＝50までの和です。x＝0［m］のところの熱流束を100000［W/m2］とするために、式38ではqw＝200000［W/m2］としています。また、図12において長さを操作していました。
時々刻々と変化する熱流束分布は次式となります（式39）。
温度分布を求めましょう。フーリエの法則から、熱流束をxで積分すれば求まります。
初期温度T（x，0）が100［degC］となるように積分定数を決めると、積分定数は以下となりました（式41）。
Copyright © ITmedia, Inc. All Rights Reserved.