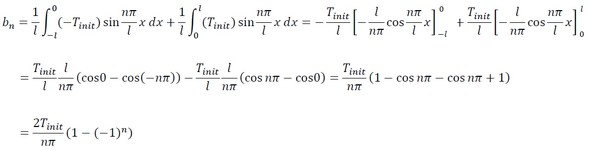時々刻々と変化する温度分布：CAE解析とExcelを使いながら冷却系設計を自分でやってみる（8）（3/6 ページ）

CAE解析とExcelを使いながら冷却系の設計を“自分でやってみる／できるようになる”ことを目指す連載。連載第8回は、非定常熱伝導問題に取り組む。

[高橋良一／ＲＴデザインラボ 代表，MONOist]

フーリエ級数を使おう

　この手の微分方程式は、フーリエ級数を使って解くことができます。そこで、フーリエ級数が使えるように少し工夫をしましょう。図3を拡張し、図4のように設定します。

　よく「x＝0の温度はどうなるのか」と聞かれるのですが、この関数をフーリエ級数で表すと必ず原点を通ります。つまり、x＝0における温度は0［degC］となります。これからはフーリエ級数によるグラフで説明します。

図4　t＝0［s］の温度分布［クリックで拡大］

　周期2lのフーリエ級数は以下でした（参考文献［1］）。

式16

式17

式18

　式9と式10の解は次式でした（式19、式20）。

式19

式20

　これを式6に代入したものが解です（式21）。

式21

　線形微分方程式に複数の解があったとしたら、それらの和も解となるので次式が成立します（式22）。

式22

　t＝0［s］のときの温度分布は次式となります（式23）。

式23

　式23は、フーリエ級数の式（式16）とそっくりです。ということは、図4の関数をフーリエ級数で表現すれば、それが初期条件（t＝0［s］）を満たす解となります。

　図4の関数は奇関数であるため、式16におけるa_nは0です。また、図4の関数は上下対称であることから、a₀＝0ですね。これは式23にも同じことがいえます。sin μxに対応するのは、sin nπ／l x（※2）なので、μ＝nπ／l（※3）となります。

（左）が※2、（右）が※3の正しい表記

式24

　t＝0［s］のときの温度分布は次式となります（式25）。

式25

　では、早速式18を計算しましょう。

式26［クリックで拡大］

　式26の（−1）ⁿは符号を反転させるために使っています。式16と式25を見ると次式が成立します（式27）。

式27

　式27を式25に代入します（式28）。

式28

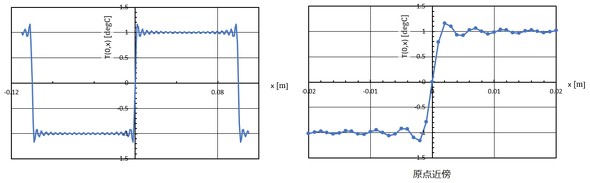
　式28を計算しましょう。図5に示します。T_init＝0［degC］とし、n＝50までの和です。サイン関数の和なので必ず原点を通ります。

図5　式28の計算結果［クリックで拡大］

　式24に式27を代入すると、時々刻々と変化する温度分布が求まります（式29）。

式29