CAEソフトに仕掛けられた2つ目のトラップ「応力特異点」を解決する：CAEを正しく使い疲労強度計算と有機的につなげる（6）（3/3 ページ）

金属疲労を起こした際にかかる対策コストは膨大なものになる。連載「CAEを正しく使い疲労強度計算と有機的につなげる」では、CAEを正しく使いこなし、その解析結果から疲労破壊の有無を予測するアプローチを解説する。連載第6回は、CAEソフトに仕掛けられた2つ目のトラップである「応力特異点」を取り上げる。

[高橋良一／ＲＴデザインラボ 代表，MONOist]

桁あってますか検算

　前述したように、計算結果の桁が数桁異なることはよくあります。例えば、［mm］単位でモデリングしたSTEP形式のファイルを有限要素法ソフトに読み込んだとき、「ソフトはその寸法値を［mm］として認識している場合」と、「［m］として認識している場合」が考えられます。それらはソフトの仕様と、STEPファイルのヘッダ情報によって変わります。ソフトが寸法値を［mm］として認識しているときはそれに応じたヤング率、［m］として認識しているときはそれに応じたヤング率を入力する必要があります。

　この確認には要素分割後の節点座標を見る必要がありますが、節点座標をテキストデータで出力するには少しソフトと格闘しなければなりませんね。3D CAD付属のCAEソフトは材質を指定するだけでヤング率などが自動設定されるので、この問題はなくなりますが、いろいろな要因で計算結果が桁外れになることはよくあることです。

　桁外れ防止のためには「桁あってますか検算」が必要です。筆者は「桁あってますか検算」を毎回行うよう習慣付けています。具体的には材料力学の範ちゅうで、手計算で応力か変位を計算し、解析結果と比較します。材料力学の範ちゅうとは以下となります（式8〜式11）。

　圧縮応力のときは座屈のチェックが必要ですね。多くの場合、式9を使うことになると思います。手計算で曲げ応力を計算して、桁があってるかを確認しましょう。……というか、「桁あってますか検算」は絶対に必要だと筆者は考えます。

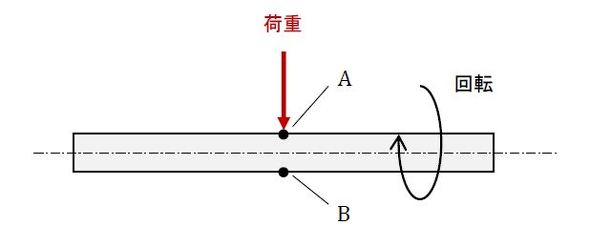
　曲げ応力の計算例を一つ紹介します。図16のような回転軸です。

図16　荷重のかかる回転軸［クリックで拡大］

　はりの曲げと考えるとA側は圧縮応力、B側は引張応力で、軸が回転するのでA点、B点の応力は圧縮と引っ張りの繰り返し応力が発生します。まさに「小野式回転曲げ疲労試験機」ですね。このようなときの「桁あってますか検算」では、軸の断面二次モーメントを計算する必要があります。

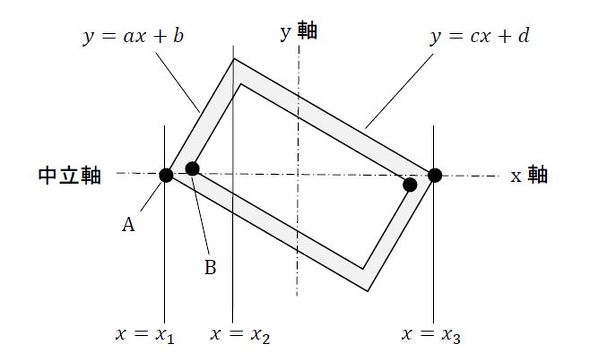
　では、図17のような角パイプだったらどうしましょうか。

図17　角パイプの断面［クリックで拡大］

　角パイプの断面二次モーメントは、外側の四角形の断面二次モーメントから内側の四角形の断面二次モーメントを引けばよかったですね。外側の断面二次モーメントは式12となります。

式12

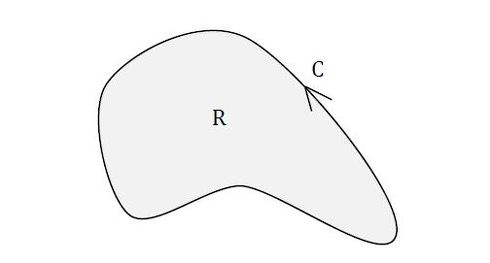
　少し面倒ですが何とかできそうです。では、内側の四角形の断面二次モーメントはというと、B点が中立軸上にないことが玉にキズです。計算する気がなくなってしまいそうです。そのようなときに便利な方法を紹介します。「グリーンの定理」（参考文献［1］）を使うのです。図18と式13をご覧ください。

図18　グリーンの定理の領域と単一閉曲線

式13

参考文献：

• ［1］矢野健太郎｜解析学概論｜裳華房（S53）

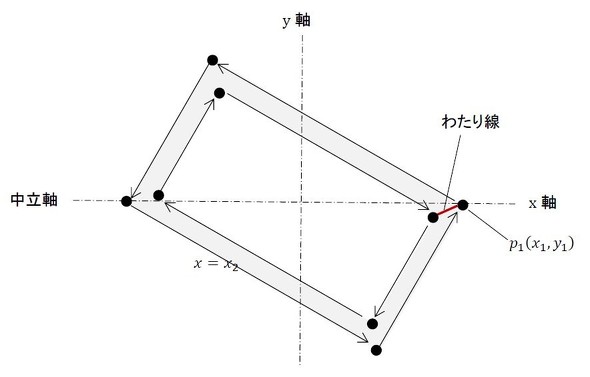
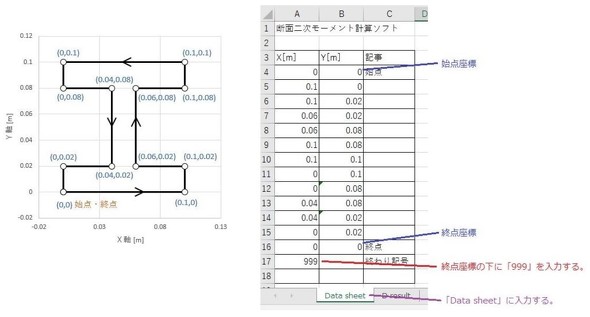
　二重積分が領域の境界線の線積分になりました。ということは、図19のように断面を一筆書きして、各点の座標値だけで積分ができることになります。一筆書きのルールは反時計回りです。空洞のある部分は時計回りです。そして、図のわたり線は「行き」と「帰り」があります

図19　断面の一筆書き［クリックで拡大］

　では、式13右辺カッコ内がちょうどy²になるような関数M（x，y）、N（x，y）を見つけて、あとは皆さん「Excel」でできますよね。

　……なんて冷たいことは言いません。筆者が用意した便利なExcelシートを紹介します。図20のような感じのものです。円弧の場合は多直線近似します。Excelシートなので簡単にできると思います。データの終わりを999にしています。これは西暦2000年問題があったときに指摘されました。やってはいけない手法ですね。

図20　断面二次モーメント計算Excelシートのイメージ［クリックで拡大］

参考文献：

• ［1］矢野健太郎｜解析学概論｜裳華房（S53）

最後に

　次回から「金属疲労」について説明します。

　ここで次のような声が聞こえてきます。「高橋さん、［mm］単位でモデリングしたなら密度の単位を［ton/mm³］にすれば大丈夫ですよ」……と。確かに、応力は期待した値となりますね。しかし、今度は［ton］という単位が混入し、はなはだ違和感があります。これは単なる帳尻合わせのようです。「それでは、密度の単位を［ton/mm³］として、モーダル解析をしたら固有振動数は大丈夫ですか？」って……そんなこと私に聞かれても知りません。　（次回へ続く）

⇒「連載バックナンバー」はこちら

Profile

高橋 良一（たかはし りょういち）
ＲＴデザインラボ 代表

1961年生まれ。技術士（機械部門）、計算力学技術者 上級アナリスト、米MIT Francis Bitter Magnet Laboratory 元研究員。

構造・熱流体系のCAE専門家と機械設計者の両面を持つエンジニア。約40年間、大手電機メーカーにて医用画像診断装置（MRI装置）の電磁振動・騒音の解析、測定、低減設計、二次電池製造ラインの静音化、液晶パネル製造装置の設計、CTスキャナー用X線発生管の設計、超音波溶接機の振動解析と疲労寿命予測、超電導磁石の電磁振動に対する疲労強度評価、メカトロニクス機器の数値シミュレーションの実用化などに従事。現在ＲＴデザインラボにて、受託CAE解析、設計者解析の導入コンサルティングを手掛けている。⇒ ＲＴデザインラボ