疲労破壊が起きない条件を考える 〜ボルトの疲労強度〜：設計者向けCAEを使ったボルト締結部の設計（2）（1/4 ページ）

部品の固定（締結）のために使用する“ボルトの設計”をテーマに、設計者向けCAE環境を用いて、必要とされる適切なボルトの呼び径と本数を決める方法を解説する。連載第2回は、疲労破壊の発生有無を予測する際に必要となる「ボルトの疲労強度」と「ボルトの締め付け条件」の検討のうち、ボルトの疲労強度の検討アプローチについて詳しく取り上げる。

[高橋良一／ＲＴデザインラボ 代表，MONOist]

　連載「設計者向けCAEを使ったボルト締結部の設計」では、設計者が使うCAE環境（設計者CAE）を用いて、必要とされるボルトの呼び径と本数を決める方法について解説することを最終目的としています。

⇒「連載バックナンバー」はこちら

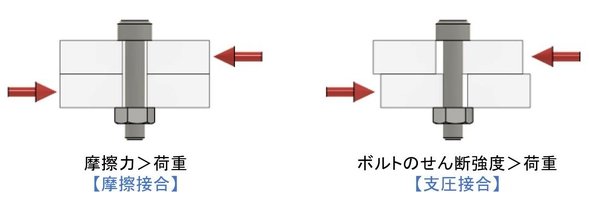
　前回お届けした連載第1回「その設計、そのボルトと本数で大丈夫？」では、ボルト締結部に要求される機能として“部品同士の結合（固定）”が重要で、その設計アプローチには「摩擦接合」と「支圧接合」があり、機械設計では摩擦接合の方が多く採用されていると述べました。

　摩擦接合を成立させるには、大きな締結力、つまりボルトを締め付けたときに発生する「軸力」が必要です。軸力が発生するということは、ボルトには「引張応力」が発生しています。そして、ボルトが装置などの固定に用いられる場合、固定されている部品には稼働する装置の振動などによる「変動荷重」が作用することになりますので、このような環境下で“疲労破壊が起きない条件”を決めなければなりません。

　疲労破壊の発生有無を予測するには、ボルトの疲労強度とボルトの締め付け条件（＝締め付けトルク）の2つの面から検討する必要があります。そこで今回は、前者のボルトの疲労強度について取り上げることにします。実は、疲労強度というのは案外と小さい値なのです。

図1　摩擦接合（左）と支圧接合（右）について ［クリックで拡大］

「ボルトの谷底はもう降伏している」

　連載開始から数えるともう38年も前になるでしょうか。「お前はもう●●でいる」という決めぜりふが有名な漫画がありましたが、いわゆる「弾性域締め付け」と呼ばれる締め付けトルクで組み立てたときも、「ボルトの谷底はもう降伏している」のです。

• 弾性域締め付け……ねじを締め付けて軸力がかかると、降伏点まではねじが軸力に比例して伸びて、軸力を除くとねじの伸びが元に戻る。この範囲（弾性域）の締め付けであれば、ねじを繰り返し使用できる
• 谷底……ねじ溝の最も深い部分のこと。これとは逆にねじ溝の最も高い部分を「山の頂」と呼び、山の頂と谷底を結ぶ面を「フランク」という

　弾性域締め付けトルクの例としては、前回も登場した「T系列」が挙げられます。T系列が弾性域締め付けであることはいずれ説明しますが、ここではT系列のトルクを採用することにします。弾性域締め付けねじ部の応力は、降伏応力の約70％とされています。もしかすると「降伏していないのでは？」と思われる方もいるかもしれませんが、この応力は公称応力、つまり“応力集中を考慮していない応力”なのです。

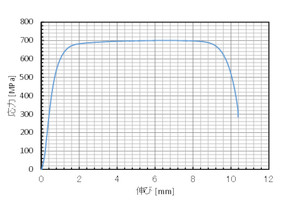
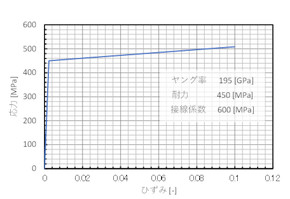
　それでは、強度区分A2-70、M12の六角穴付きステンレスボルトで応力を調べてみましょう。A2-70ボルトの引張強さ（引張強度）は700［MPa］で、耐力は450［MPa］です。ステンレスボルトの応力は図2のように降伏点が明瞭に表れませんが、降伏の目安となる耐力として450［MPa］を使ってよさそうです。図2の横軸は引張試験機の変位で正しいひずみでないことはご容赦ください。また、接線係数は600［MPa］を採用することにします。解析ソフトウェアに材料定数として入力する「応力−ひずみ線図」は、図3のようになります。

図2　A2-70ボルトの引張試験結果（左）／図3　解析に使用する「応力−ひずみ線図」（右） ［クリックで拡大］

　摩擦係数を0.15［-］とし、M12六角穴付きステンレスボルトをT系列のトルク42［Nm］で締め付けたときの軸力は17500［N］なので、これを引張荷重とします。

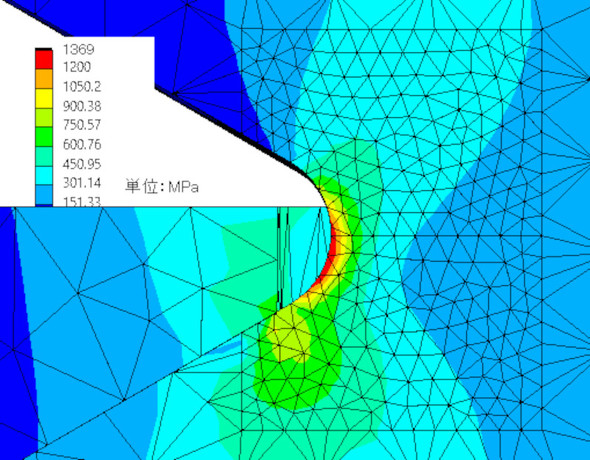
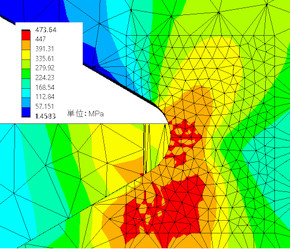
　まずは、弾性体として解析します。その結果、図4に示すように弾性域締め付けであるのに、谷底の応力は1369［MPa］と降伏応力を超えてしまっています。

図4　ねじ谷底のミゼス相当応力（弾性解析） ［クリックで拡大］

　ねじ谷底の曲率半径Rが気になります。ここでは大きめに考えて、谷底のRがめねじ山と干渉しないギリギリの値（以下の式に示す値）でモデリングしました。

R＝0.144×ピッチ＝0.144×1.75＝0.252［mm］

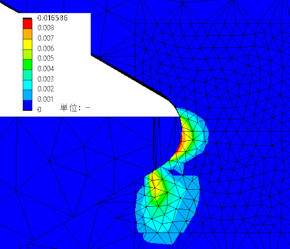
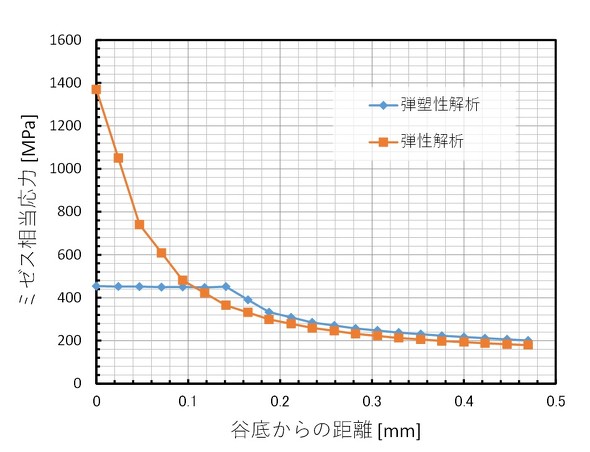
　さて、今度は図3で示した応力−ひずみ線図に従って、弾塑性解析をしてみましょう。結果は図5のようになりました。確かに応力は耐力である450［MPa］を超えていますが、塑性範囲がよく分かりません。では、相当塑性ひずみを見てみましょう。ひずみには「弾性ひずみ」と「塑性ひずみ」があります。塑性ひずみ成分だけを取り出し、相当塑性ひずみ分布としたものを図6に示します。谷底は確かに塑性変形していることが分かります。図7に谷底からの距離とミゼス相当応力の関係を示しておきます。

図5　ねじ谷底の相当応力（弾塑性解析）（左）／図6　ねじ谷底の相当塑性ひずみ（右） ［クリックで拡大］

図7　谷底からの距離とミゼス相当応力の関係 ［クリックで拡大］

　いくつかの文献や論文では、ボルト谷底の応力集中係数αについて議論されていますが、谷底は既に塑性変形しており、谷底の応力は降伏点に達しています。よって、弾性解析した応力値、つまり「α×公称応力」はあまり意味を持たず、応力集中係数αはもはや無用で、切り欠き係数βを導入する必要があると考えられます。

　ねじ谷底のRはキッチリ決まっているわけではなく、「JIS B 0209-1」によれば、

強度区分8.8以上において、0.125×ピッチより小さくなってはならない

としかありません。「谷底は塑性変形しているので、その応力は降伏応力ないしは耐力にほぼ等しく、谷底のRにあまり影響を受けない」というと少し言い過ぎかもしれませんが、締結部の設計において、谷底のRはあまり気にする必要はなさそうです。そもそも、市販品のボルトを使用することが多いので、谷底のRは設計者が指定できず、入荷した品物に従うことになります。

　応力の単位については［N/mm²］ではなく［MPa］で表記しています。同じ値なのですが、筆者なりの理由があって［N/mm²］を使っていません。この件についてはいずれ説明したいと思います。