領域最適化の実践：フリーFEMソフトとExcelマクロで形状最適化（13）（5/5 ページ）

原理原則を押さえていれば、高額なソフトウェアを用意せずとも「パラメトリック最適化」「トポロジー最適化」「領域最適化」といった“形状最適化”手法を試すことができる！　本連載ではフリーのFEM（有限要素法）ソフトウェア「LISA」と「Excel」のマクロプログラムを用いた形状最適化にチャレンジする。連載第13回では、LISAとExcelのマクロプラグラムを使って、実際に領域最適化を行う。

[高橋良一／ＲＴデザインラボ 代表，MONOist]

片持ちはり領域最適化（続き）

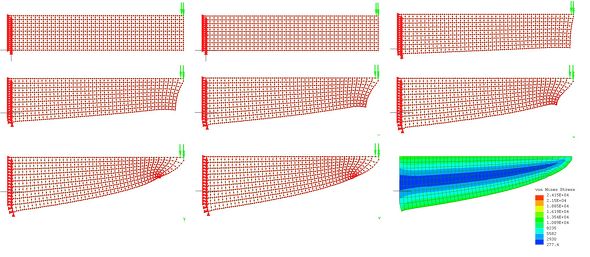
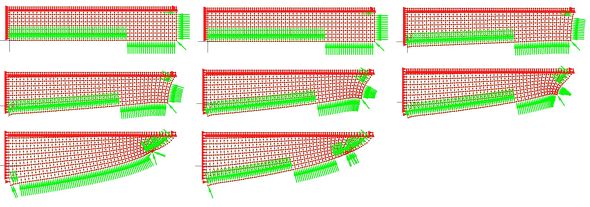
　前述した作業を計8回繰り返します。形状変化の過程を図26に示します。図26の右下に相当応力図を示します。相当応力が緑色になって応力が均一化されていることが分かります。図27に形状変更を与える荷重を示します。

図26　形状変化の過程［クリックで拡大］

図27　形状変更を与える荷重［クリックで拡大］

　9回目の最適化でLISAの計算は失敗します。というのも、8回目で最適化は完了しており、これ以上形状を変更する必要はないのですが、連載第12回の式3に示すように、領域寸法の0.04倍だけ形状を変化させるような荷重が設定されますので、余計な形状変化が生じるためです。

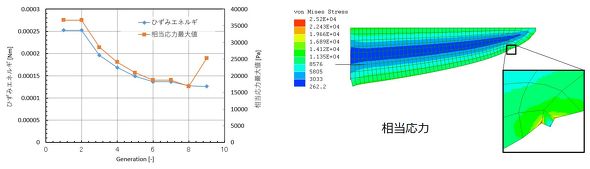
　図28に、ひずみエネルギーと相当応力の変化を示します。世代が進むにつれてひずみエネルギーは極小値に進み、相当応力最大値も低下します。第9世代で相当応力最大値が増加したのは、図28右図における形状の急激な変化部による応力特異点のためです。ここはもともと第1世代の右下の角の要素でした。

図28　ひずみエネルギーと相当応力の変化［クリックで拡大］

最適化形状を調べる

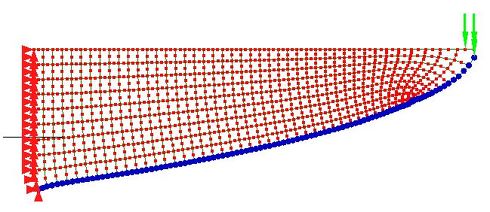
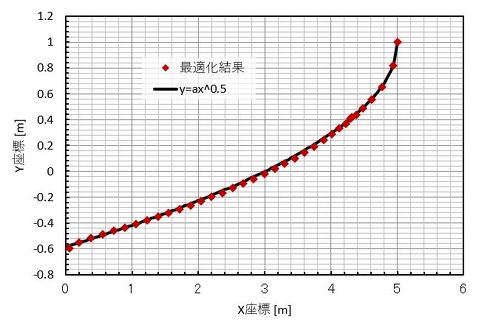
　最適化後の形状を調べましょう。第9世代の形状を図29に、選択した節点の座標をプロットしたものを図30に示します。図30にはy＝a√xのグラフを重ねています。片持ちはりの高さ寸法がa√xになるのは連載第2回で話した平等強さのはりでした。今回の最適化形状と平等強さのはりの形状が一致しました。

図29　第9世代の形状［クリックで拡大］

図30　第9世代の形状とy＝a√xのグラフ［クリックで拡大］

　以上のように、片持ちはりの領域最適化では、剛性最大化、つまり、ひずみエネルギー最小化と、応力平準化を両立する解が得られました。剛性最大化の解が応力平準化の解と等しいということを証明する数学力は筆者にはありませんが、今まで何回か申し上げたように、両者は“お隣さん”のようです。次回は、いろいろなケースの領域最適化に挑戦してみます。お楽しみに！　（次回へ続く）

⇒ 連載バックナンバーはこちら

Profile

高橋 良一（たかはし りょういち）
ＲＴデザインラボ 代表

1961年生まれ。技術士（機械部門）、計算力学技術者 上級アナリスト、米MIT Francis Bitter Magnet Laboratory 元研究員。

構造・熱流体系のCAE専門家と機械設計者の両面を持つエンジニア。約40年間、大手電機メーカーにて医用画像診断装置（MRI装置）の電磁振動・騒音の解析、測定、低減設計、二次電池製造ラインの静音化、液晶パネル製造装置の設計、CTスキャナー用X線発生管の設計、超音波溶接機の振動解析と疲労寿命予測、超電導磁石の電磁振動に対する疲労強度評価、メカトロニクス機器の数値シミュレーションの実用化などに従事。現在ＲＴデザインラボにて、受託CAE解析、設計者解析の導入コンサルティングを手掛けている。⇒ ＲＴデザインラボ