トポロジー最適化ってどうなってるの？ どうやるの？：トポロジー最適化とは何か（2）（1/2 ページ）

[水野操 mfabrica合同会社 社長／3D-GAN，MONOist]

　皆さん、こんにちは。1カ月たつのは早いものでもう6月。そして、皆さんが大好きな？　「設計・製造ソリューション展」の季節ですね。さて、前回は異なる最適化の種類とその違いについてお話をさせていただきました。今回は、「そもそもトポロジー最適化の背景にあるものは何か」ということと、基本的な流れについてお話します。

トポロジー最適化の定義とは

　あらゆるCAEのソフトの裏には理論があって、その理論が実装されているのがCAEのソフトであるわけです。もちろん、トポロジー最適化もそうです。トポロジー最適化では、何らかの設計変数を使って材料分布を求めていくわけなのですが、その方法にはいくつかの種類があります。主なものとしては「均質化法」「レベルセット法」「密度法」と呼ばれるものがあって、現在提案されてきている手法というのは、だいたいこれらのどれかに当てはまるようです。

　今回は構造最適設計ソフトウェア「OPTISHAPE-TS」（くいんと）を使ってみます。この事例では、密度法を用いて最適な材料配置を求める最適化を実行します。これは「要素の密度分布を確認して、部材が必要な部分といらない部分を判断する」ということなのです。

　ある物体を考えた時に、節点密度を設計変数として考えますが、その時の密度をρとして、ρが0.0であれば材料がいらない部分、密度が1であれば必要な部分として考えるわけです。

　トポロジー最適化の計算結果と実際の製品の形が結構一致しているものは案外あるもので、橋梁設計だったり、サッカー場の構造のレイアウトだったり、あるいは下記に示すような自転車のフレーム構造を考えてみたりとか、トポロジー最適化の考え方を使ってみると「なんであの構造が、あんな形をしているのかなぁ」ということが見えてきて面白いですよね。

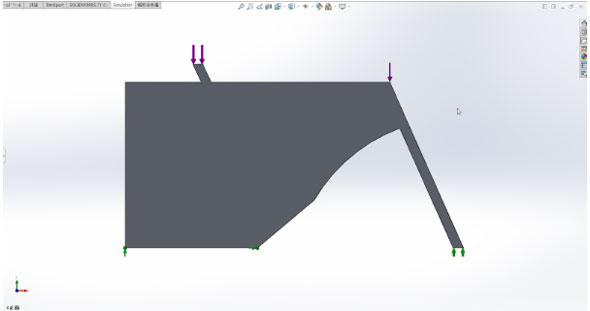
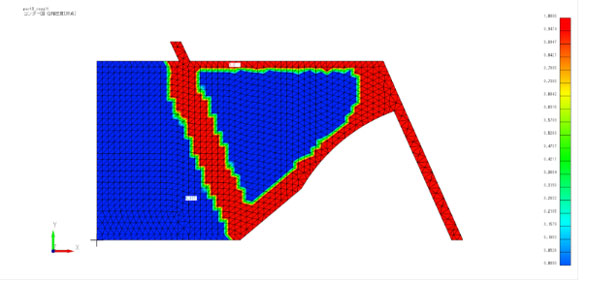
　取りあえず設計領域を3D CADで作成して、メッシュや境界条件を作成してみた結果が以下です。

メッシュや境界条件を作成する

トポロジー最適化をやったところ、自転車のフレームの三角形の形が求められた

　私もまだまだ経験不足でどうも設定がきちんとできていないので、まだ思ったような結果が得られていないのですが、それでもこうすることで力の流れを可視化することができるメリットはとても大きそうです。

トポロジー最適化の特徴とは

　トポロジー最適化の特徴ってあらためて考えてみると何でしょうか。もちろん、位相の最適化なのですが、結果として何が起きるのかというと、要するに構造に不必要な部材を削除してしまうということになります。つまり、形状最適化や寸法最適化と比較すると最初の形状とは似ても似つかないほど大きく形が変わってしまうことも珍しくはないのです。

　ここから何が見えてくるでしょうか。例えば、デザインに対するインスピレーションになるかもしれません。工業製品のデザインは「格好がよいもの」を作っても、それが工業製品としてのパフォーマンスを満たしていなければなりません。そういう意味では構造的なリミテーションをデザインをする前に把握しておくためのヒントになりえますね。

　また、それは設計者にとっても意味があります。「材料が残っている部分」というのは、まさに「力が流れていく」とも言い換えることができます。つまり荷重の伝達経路が如実に残っているということが言えますね。だから、この部分をしっかりおさえた設計をすれば、最初から最適な部品形状が作れる可能性があるといえます。

　もちろん、最適化をやる際には、どこが設計領域であるのかをソフトに教えてやる必要があります。肝心なところを領域に含めていないと、その部分は最適化ができないので、製品開発者としては特にどの部分を解析対象に含めるのかは引き続き重要なところです。

最適化の基本的な流れ

　今回は実際に、簡単な構造物を最適化してみたいと思います。具体的にはオリジナルの体積の60％の重量で、引き続き必要な剛性を維持する形状を考えていきます。また、オリジナルの形状と同様に断面方向に対しては等断面となるように制限を加えたいと思います。

　さて、詳しいことはまた次回以降に考えてみたいと思うのですが、最適化において考えなければいけない関数が2つあります。その1つ目が「目的関数」です。関数というと何気に難しく聞こえますが、目的関数とは簡単にいうと、「その数値を最小化したい」という類のものです。例えば、「その部品の体積を最小化したい」みたいなものですね。参考までに「剛性を最大化したい」というようなものは「コンプライアンスを最小化したい」と言い換えられます。

　もう1つの関数が「制約関数」というものです。いくら目的を達成するといっても目的のためには手段を選ばないではないとか、どんな状況を経験してもその目的を達するということではないことがほとんどだと思います。大体において最適化の過程で何らかの数値を一定値にキープしたいとか、この数値以下にしたいというものがあると思います。そのような関数を制約関数といいます。

　とまあ、「それだけ聞いていても何のこっちゃ」ということになるので、実例を示しながらプロセスについて考えてみます。