領域最適化のアルゴリズムについて考える:フリーFEMソフトとExcelマクロで形状最適化(12)(1/6 ページ)
原理原則を押さえていれば、高額なソフトウェアを用意せずとも「パラメトリック最適化」「トポロジー最適化」「領域最適化」といった“形状最適化”手法を試すことができる! 本連載ではフリーのFEM(有限要素法)ソフトウェア「LISA」と「Excel」のマクロプログラムを用いた形状最適化にチャレンジする。連載第12回では、前回に引き続き「領域最適化」をテーマに具体的なアルゴリズムについて考えながら、その理解を深めていく。
「力法(traction method)」の具体的な方法を説明していきましょう。なお、次回の解説でフリーFEMソフト「LISA」のファイルと「Excel」のマクロプログラムを配布しますが、本稿を読めば自分でプログラムが書けるようになると思います。
前回の記事で最も重要な式を以下に示します(参考文献[1])。
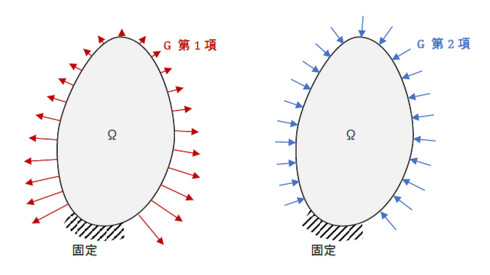
「形状勾配関数」と命名されたG(ベクトル量)に比例する力(図1)を領域の輪郭に与えて弾性解析すると、変形後の形状による目的関数(物体に蓄えられる仕事量)は、前の世代の目的関数よりも小さくなるので、この作業を繰り返せば目的関数を最小化できます。正確には、目的関数が極小値を複数持っている場合はその1つが求まることになります。
領域最適化のアルゴリズム
式1の第1項はひずみと応力の積でした。連載第5回の式23と同じで、結局、応力の二乗になるので圧縮応力でも引張応力でもプラス値となります。ひずみと応力の積を使ってもいいのですが、直感的に分かりやすい値として相当応力を使うことにしましょう。相当応力も常にプラス値なので、それほど悪い近似ではないと思います。
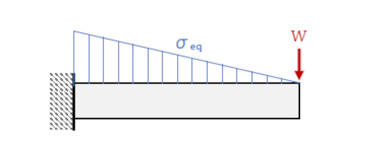
「片持ちはり」を例に考えてみましょう。片持ちはりの応力分布を図2に示します。はりの表面の応力は引張応力なのですが、せん断応力がゼロなので引張応力は相当応力σeqと等しくなります。
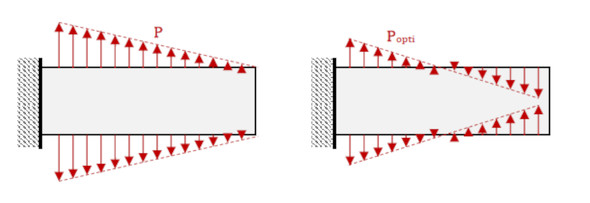
この応力に比例した荷重を輪郭に印加すると、荷重Pは図3左図のようになります。なお、太字はベクトルを表しています。
う〜ん。荷重が全部外向きなので最適化対象の体積が増加してしまいます。では、式1の第2項のΛについて考えましょう。
目標応力σtargetを決めましょう。そして、荷重Poptiを次式としましょう。nは輪郭の外向き法線ベクトルです。
σnode:節点の相当応力、ただし要素解[Pa](要素解と節点解は巻末で説明する)
Pcoefficient:比例定数[N]
式2を外力とした場合を図3右図に示しています。応力の大きな部分は肉厚を大きくし、応力の小さな部分は減肉する方向に変形させる荷重となりました。今まで難しいことを書いてきましたが、誰でも思い付く発想に落ち着きました。
比例定数Pcoefficientは109のオーダーか、1桁台か、10-9のオーダーか見当も付きませんので、次式で決めることにしました。
Pratio:人間が決める定数[-]
disprange:次世代の最適形状を求める解析での節点変位の最大値の絶対値
noderange:節点座標の最大値−最小値、最適化対象の大きさのこと
図3右図の荷重による解析結果で、たまたまdisprange=0.05[m]、noderange=1.00[m]だったとしましょう。この場合、最適化対象の大きさが1[m]で、1世代進むごとに領域の輪郭は最大0.05[m]移動します。これくらいの変化量が妥当なところでしょう。Pratioを0.05[-]としておけば、Pcoefficient newはPcoefficient oldと等しくなります。
違うケースを考えましょう。もし、disprange=0.01[m]だったら領域の輪郭移動量が小さく、なかなか最適化が進まないのでスピードアップが必要です。Pratio=0.05[-]としておけば、式3によると、Pcoefficient newはPcoefficient oldの「5倍」となって、次の解析による変形量は5倍大きくなります。Pratioはそのような定数で0.05[-]くらいにしておくとよいと思います。Pcoefficientの初期値は少なめにして、10000[N]としています。
Copyright © ITmedia, Inc. All Rights Reserved.