非線形に入る前に、線形有限要素法について復習しておく：いまさら聞けない 非線形構造解析入門（2）（5/5 ページ）

多くの3D CADではオプションとしてCAE機能が用意されているが、多くの方が「線形解析」での利用にとどまっており、「非線形解析」にまで踏み出せていない現状がある。本連載では、構造解析でも特に非線形解析にフォーカスし、初心者向けに分かりやすくその特長や活用メリットなどを紹介する。連載第2回では「非線形」の話題に入る前に、あらためて「線形有限要素法」について確認する。

[水野操 mfabrica合同会社 社長／3D-GAN，MONOist]

5．マトリクスの求解（連立1次方程式を解く）

　構築された全体剛性マトリクスと荷重ベクトルから、連立1次方程式を解いて、未知数である変位uを求めます。当然ながら、皆さんが実際に解く解析モデルは非常に自由度数の多いモデルですから手計算で解くわけにはいきません。コンピュータのプログラムで解くことになります。このような連立1次方程式を解くプログラムのことを、一般的に「マトリクスソルバー」と呼びます。

　マトリクスソルバーにはさまざまなものが提唱されており、多くの商用解析ソフトでは、複数のソルバーが組み込まれていることも珍しくなく、そのうちの1つがデフォルトのソルバーになっています。マトリクスソルバーは基本的に、「直接法」と呼ばれるものと、「反復法」と呼ばれるものに大別されています。

　直接法のソルバーは、連立方程式を直接消去するタイプのソルバーで、マトリクスが非正定でない限り必ず解くことができ（条件が悪いと解の精度が悪化することはあります）、安定的に解けるため、多くの商用ソフトでは一般的に直接法がデフォルトになっていると思います。一方、直接法ソルバーのデメリットは、メモリの消費量が多くなることや計算時間が増えがちなことで、大規模な問題では注意が必要です。

　一方、反復法のソルバーは、初期値を推定し、十分に収束するまで反復計算を行って、近似解を求める手法です。反復法は直接法と比べると、必要なメモリと計算時間が少なくて済むケースが多いのですが、マトリクスの状態が悪いと、反復回数が増大して計算時間が増えてしまうことも考えられます。反復法が効率的かどうかは、解析する問題の内容にも依存するところがあるので、もし、ソルバーの特徴を十分に把握していないようであれば、直接法のソルバーを使った方がより確実だと思います。

6．応力などの結果の算出

　マトリクスの求解をすることで得られるのは、要素の節点の変位です。では、節点の変位から、解析結果としておなじみの応力やひずみなどの情報はどのようにして得られるのでしょうか？　ここで登場するのが、前述した、応力・ひずみ関係式（{σ}＝[D]{ε}）や、ひずみ・変位関係式（{ε}＝[B]{u}）です。

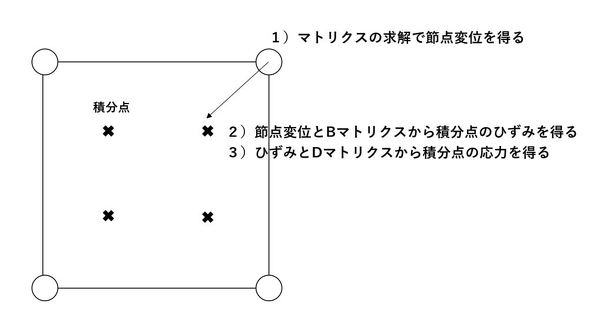
　以下のような要素を考えてみます。

図6　応力などの結果の算出［クリックで拡大］

　まず、得られた節点変位とBマトリクスから、要素の積分点におけるひずみを得ることができます。ひずみが要素の積分点における値であるのは、ガウスの数値積分の都合によります。ひずみを得たら、今度は、今得られたひずみとDマトリクスから、積分点における応力を得ることが可能です。

　ということで、少し長くなりましたが、以上で線形有限要素法プログラムの計算の流れを紹介しました。

　ただ、あくまでも“ざっくりとポイントをかいつまんで説明した”にすぎません。解析プログラムを組んだことがある人からすれば、ごく当たり前の内容だったかと思います。もし、「もっと詳しく、厳密に知りたい」という方は、有限要素法に関する専門書などを読んでみるとよいでしょう。

　次回から「非線形」の話に戻りたいと思います。お楽しみに！　（次回へ続く）

⇒ 連載バックナンバーはこちら

Profile

水野 操（みずの みさお）

1967年生まれ。mfabrica合同会社 社長。ニコラデザイン・アンド・テクノロジー代表取締役。3D-GAN理事。外資系大手PLMベンダーやコンサルティングファームにて3次元CADやCAE、エンタープライズPDMの導入に携わった他、プロダクトマーケティングやビジネスデベロップメントに従事。2004年11月にニコラデザイン・アンド・テクノロジーを起業し、オリジナルブランドの製品を展開。2016年に新たにmfabrica合同会社を設立し、3D CADやCAE、3Dプリンタ関連事業、製品開発、新規事業支援のサービスを積極的に推進している。著書に著書に『絵ときでわかる3次元CADの本』（日刊工業新聞社刊）などがある。