ラグランジュの方程式(その1)〜仮想仕事の原理と一般座標・一般力〜:1Dモデリングの勘所(39)(1/3 ページ)
「1Dモデリング」に関する連載。連載第39回では「ラグランジュの方程式(その1)」と題し、仮想仕事の原理と静的問題への適用例を示した後、ラグランジュの方程式の基礎となる一般座標と一般力について説明する。
運動方程式を機械的に解く方法として、「ラプラス変換」があることを連載第36回で紹介した。
一方、運動方程式の導出は通常、対象物に作用する力とモーメントを考えて、「ニュートンの運動の第2法則」を適用して実施する。しかしながら、連載第38回で取り上げた回転2関節機構のように、自由度が複数あり運動が複雑な場合は通常の方法で運動方程式を導出するのは容易ではなく、誤りが発生する可能性も高い。
このような場合に、機械的に運動方程式を導出する方法として「ラグランジュの方程式」がある。ラグランジュの方程式は「仮想仕事の原理」を基本に、系のエネルギーを考えることによって運動方程式を導出する。
今回は仮想仕事の原理、この静的問題への適用例を示した後、ラグランジュの方程式の基礎となる「一般座標」「一般力」について説明する。
仮想仕事の原理
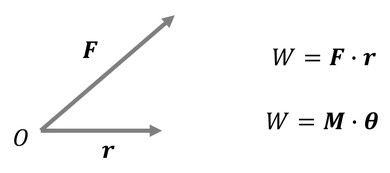
まずは「仕事」の定義について、図1を例に説明する。
図1において、質点Oに力Fが作用し、質点の位置がrだけ変化したとき、力Fは質点に対して、
の仕事を行ったいえる。式1はベクトル表示であるが、力方向と変位の方向との間の角度をαとすると、W=Fr cos αとなる。また、回転運動の場合にはモーメントをM、角変位をθとすると、ベクトル表示で、
となる。仕事の単位は上式から明らかなように、kg・m2・s-2で、これを組立単位で「J(ジュール)」と呼ぶ。また、上式の定義から分かるように仕事はスカラー量である。
次に、静的なつり合い状態からの仮想的な動き(δrおよびδθ)を考えたときの仮想的な仕事は、仕事の定義から、力(モーメント)と変位(角変位)の方向が同じ場合、
となり、これを「仮想仕事」と呼ぶ。
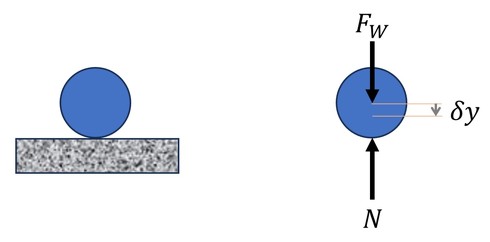
一方、静的につり合い状態にある物体では、物体の仮想的な動きに対する全ての力およびモーメントによる仮想仕事の代数和は0となる。これが仮想仕事の原理である。図2を用いて説明する。
図2のように、床面に質点(ボール)が置いてある状態で、δyなる仮想変位を考えると、仮想仕事は、
となり、これに仮想仕事の原理を適用すると、
となり、FW=Nが導かれる。
Copyright © ITmedia, Inc. All Rights Reserved.