機構制御系のモデリング(その1) 〜機構と制御の基本について考える〜:1Dモデリングの勘所(36)(1/4 ページ)
「1Dモデリング」に関する連載。連載第36回では「機構制御系のモデリング(その1)」と題し、機構と制御の基本について考える。
機構制御系のモデリングについて考える。今までに扱った熱、流れ、音振動といった現象は状態量のフローを考えることにより、似たような方法でモデリングが可能であった。
一方、機構、制御は製品を構成する要素として非常に重要ではあるが、そのモデリングの方法はこれまで扱ってきた対象とは若干異なる。機構も制御もその専門の書が存在するが、多くはいきなり専門用語が出てきて、門外漢にとってその本質を理解することは容易ではない。
しかし、よく観察してみると、機構は力学を基本としており、制御は振動との相性が高い。そこで、ここでは機構制御系を力学、振動の視点から捉えることにする。今回はその1として、“機構と制御の基本”について考える。
機構と制御
最初に、「機械」「機構」「制御」の言葉の定義について整理したい。
- 「機械」とは、動力を受けて、目的に応じた一定の運動/仕事をするもの
- 「機構」とは、機械などの諸部分が互いに関連して働く仕組みで、機械の内部構造、メカニズムを指す
- 「制御」とは、注目している対象物に属する、注目している動作が、何らかの目的とする動作になるよう、その対象物に操作を加えること(参考文献[1])
以下、この定義を念頭に置き、これらをどう式に展開していくかを考える。
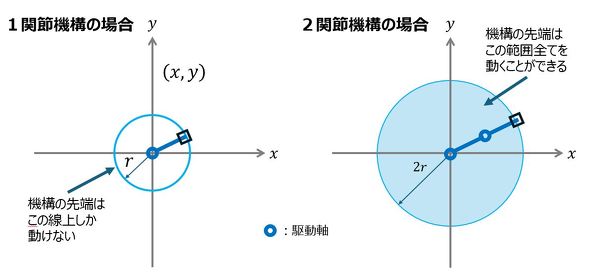
図1に機構制御系の例を示す。
図1左図は1関節機構で原点に駆動軸があり、機構先端はリンクの長さをrとすると、半径rの軌道上を動くことができる。この際、駆動軸にあるモーターの入力を制御することにより、機構先端を所定の位置に、所定の時間で移動させることができる。
一方、図1右図は2関節機構で関節が1つ増えただけで、機構先端の動ける範囲は、2つのリンクの長さが同じrとすると、半径2rの円の内部の全ての位置となる。1関節機構では半径rの円周上しか動けなかったのに対し、2関節機構では半径2rの円の内部全てが可動範囲となり、自由度が飛躍的に増す。このように“機構とは、複数の部品を互いにうまく関連して動くようにすることにより、単独部品を凌駕する機能を実現するもの”と定義することもできる。
参考文献:
- [1]足立修一|制御工学の基礎|東京電機大学出版局(2016)
機構の基本
機構問題を扱うには、大きく2つの方法がある。1つは、機構の動きのみを考えるもので「運動学(Kinematics)」と呼ばれる。もう1つは、機構が運動する際の慣性力を考慮したもので「動力学(Kinetics)」と呼ばれる。動力学で慣性力を無視したものが運動学ともいえる。
また、図1の各関節に動きを与えて、先端の位置を求めることを「順問題」という。一方、機構先端の位置を所定の動きにするための、各関節の動き(動力学の場合には駆動トルクも)を求めることを「逆問題」という。今回は、運動学について説明する。
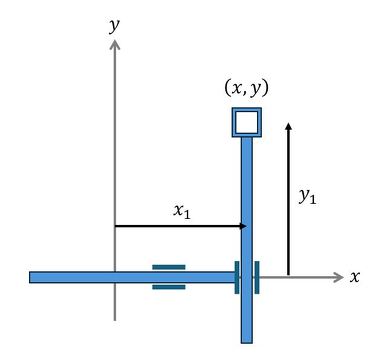
図2に示す直動2関節機構で考えてみる。(x,y)は機構先端の座標、(x1,y1)は駆動軸の移動変位である。
駆動部を(x1,y1)だけ動かしたら、先端(x,y)の位置はどうなるかを考えるのが運動学の順問題である。この場合は、
となる。一方、先端の位置を(x,y)にするためには駆動部(x1,y1)をどう動かしたらいいかを考えるのが逆問題で、この場合は、
となる。このように、直動2関節機構の運動学の順問題、逆問題は難なく解くことができる。3次元空間を駆動領域とする直動3関節機構も同様に解くことができる。
Copyright © ITmedia, Inc. All Rights Reserved.