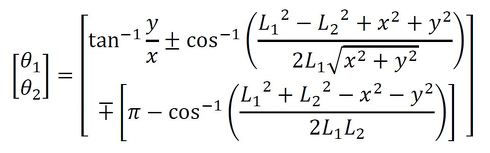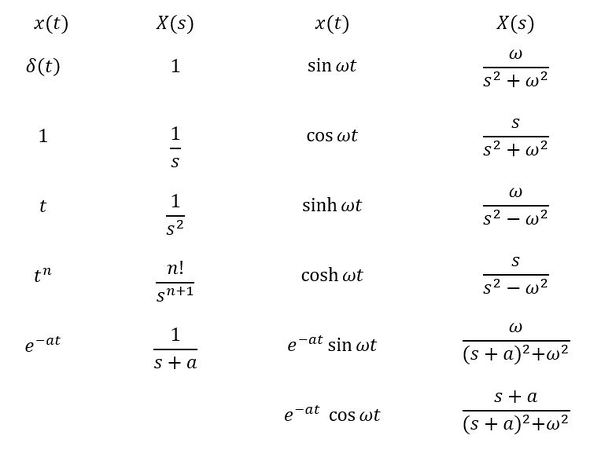機構制御系のモデリング（その1）～機構と制御の基本について考える～：1Dモデリングの勘所（36）（2/4 ページ）

「1Dモデリング」に関する連載。連載第36回では「機構制御系のモデリング（その1）」と題し、機構と制御の基本について考える。

[大富浩一／日本機械学会設計研究会，MONOist] PC用表示関連情報

LINE

Hatena

前のページへ | 次のページへ

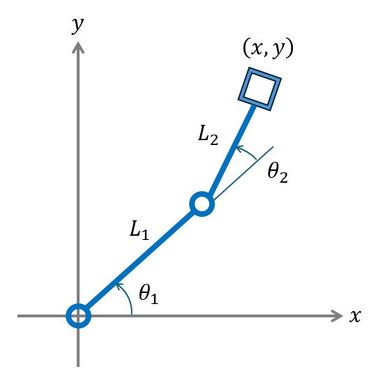
　次に、図3に示す回転2関節機構について考える。

図3　回転2関節機構［クリックで拡大］

　リンク1の長さをL₁、リンク2の長さをL₂、第1関節の角変位をθ₁、第2関節の各辺をθ₂とすると、先端（x，y）の位置は、

式3

となる。これが、回転2関節機構の運動学の順問題の解となる。

　図3の順問題を「Modelica」で表記すると以下のようになる（リスト1）。なお、各関節は初期状態で0とし、1秒間で半時計方向に一定角速度で回転するものとする。

model twoLinkStaJun
import Modelica.Constants.pi;
import Modelica.Constants.g_n;
Real theta1;
Real theta2;
Real x;
Real y;
parameter Real L = 2;
parameter Real omg1=2*pi;
parameter Real omg2=2*pi;
equation
x = L*cos(theta1) + L*cos(theta1+theta2);
y = L*sin(theta1) + L*sin(theta1+theta2);
cita1=omg1*time;
cita2=omg2*time;
end twoLinkStaJun;

リスト1　Modelicaでテキスト表現した場合

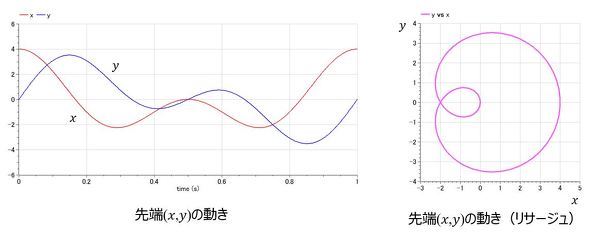
　リスト1を解析した結果を図4に示す。図4左図は先端（x，y）の位置の各座標の動きを、図4右図は横軸に座標x、縦軸に座標yをとって先端の動きを示した、いわゆるリサージュを示す。

図4　回転2関節機構の順問題の解の例［クリックで拡大］

　図3で、先端の位置を（x，y）にするために駆動部（θ₁，θ₂）をどう動かしたらいいかを考えるのが逆問題で、直動2関節機構の場合とは異なり、簡単には求まらない。結果だけ示すと式4のようになる。

式4

　すなわち、解が複数（2個）存在する。このように、機構が複雑になると逆問題は解が複数となり、工夫が必要となる。

ラプラス変換

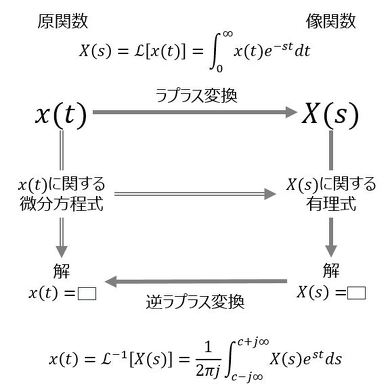
　制御の基本に入る前に、運動方程式の解法の一つである「ラプラス変換」ついて説明する。通常、運動方程式を解く際は、その一般解を求め、これに含まれる積分定数を、初期条件を満足するように定める。このように、都度異なる運動方程式に対して、それらに適応した一般解を求めるのはそれなりの経験が必要である。こうした手順を回避し、運動方程式を機械的に解く方法がラプラス変換である。図5にその手順を示す。