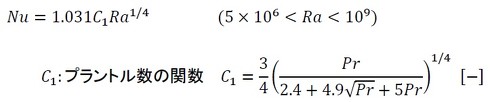ダクトに巻く断熱材を設計する：CAE解析とExcelを使いながら冷却系設計を自分でやってみる（18）（1/3 ページ）

CAE解析とExcelを使いながら冷却系の設計を“自分でやってみる／できるようになる”ことを目指す連載。連載第18回は、ダクトに巻く断熱材の設計計算Excelシートを作成する。

[高橋良一／ＲＴデザインラボ 代表，MONOist]

　太いパイプに高温の液体やガス、あるいは低温の液体が流れている場合、パイプの周囲に「断熱材」を巻き付けます。断熱材は、高温の流体に対しては熱を逃がさない役割を、低温の流体に対してはダクトの表面が結露しないようにする役割を担います。

　今回は、ダクトに巻く断熱材の設計計算Excelシートを作成してみましょう。

⇒「連載バックナンバー」はこちら

ダクトに巻く断熱材

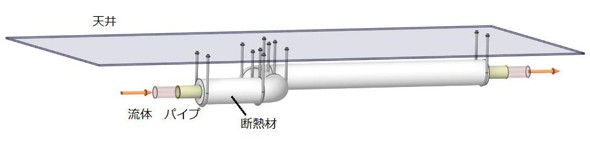
　図1に、ダクトの一例を示します。

図1　ダクトの例［クリックで拡大］

　ダクトは、天井から吊り下げられるケースがほとんどのようです。断熱材の外側には銀色のシートを被せることが多くあります。この銀色のシートの役割については、連載第7回の「ふく射」の項で説明しましたね。

　流体の温度が与えられているとき、熱の逃げる量を目標値以下に抑えるためには、断熱材の厚さをいくらにすべきかが問題となります。また、断熱材の表面温度を目標値以下にするには、やはり断熱材の厚さが重要な要素になります。

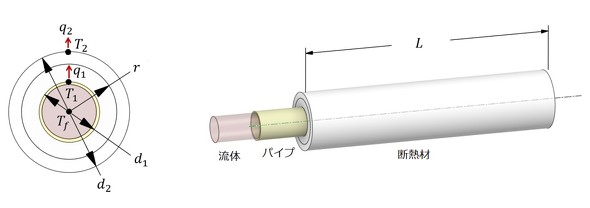
　図2に、解析モデルを示します。

図2　解析モデル［クリックで拡大］

　断熱材内側の直径をd₁、温度をT₁、熱流束をq₁、断熱材外側の直径をd₂、温度をT₂、熱流束をq₂とします。また、パイプ内の流体温度をT_f、主流の温度（室温）をT_∞とします。

　連載第15回のコイル設計において、ホローコンダクター内の温度変化はほぼゼロでした。金属パイプと断熱材の熱伝導率は桁違いで、金属パイプの方が圧倒的に大きいため、金属パイプ内の温度変化もほぼゼロです。よって、流体温度T_fと断熱材内側の温度T₁は等しいとします。

　では、計算式を導いていきましょう。ダクトの場合、与えられているのは主流の温度とパイプ内の流体の温度です。ここでは、主流の温度側から攻めていきましょう。主流の温度と断熱材外側の温度との差は、式1で表されます。

式1

　熱伝達率を求める必要があります。ダクトの場合、外部流れの自然対流熱伝達となるため、前回紹介した式が使用できます。グラスホフ数Grとレーレー（またはレイリー）数Raは、次の式で計算します（参考文献［1］）。

式2

式3

　水平に置かれた円柱の熱伝達率は実験式があり、次の式で表されます（参考文献［1］）。

式4

式5

　熱伝達率は、式6となります。

式6

連立方程式を解く

　式はそろいましたが、未知数が複数あるため、連立方程式を解く必要があります。前回は通過熱量が分かっていたため比較的簡単でしたが、今回は熱通過量が未知数となります。また、式4と式5の形から解を陽の形で導くことは難しいようです。

　この計算は少し骨が折れますが、Excelシートを作成する準備を進めましょう。断熱材を通過する熱量をQ［W］とした場合、温度と通過熱量の関係は、連載第5回の式22で求めることができます。

式7

　断熱材外側の熱流束は、式8で表されます。

式8

　この式8を式1に代入します。

式9

　ここで、未知数をT₂−T_∞とします。

　分子のカッコ内に−T_∞とT_∞を加えることで、式9は以下のようになります。

式10

　式4およびヌセルト数の定義から、熱伝達率は式11で表されます。

式11

　式11を式10に代入し、変形します。

式12

　式12を、レーレー数が10^-8≤Ra≤5×10⁶の範囲の方程式とします。

　続いて、レーレー数が5×10⁶＜Ra＜10⁹の範囲の方程式を作成します。式5とヌセルト数の定義から、熱伝達率は式13で表されます。

式13

　この式13を式10に代入し、変形します。

式14

　式14は、レーレー数が5×10⁶＜Ra＜10⁹の範囲における方程式とします。