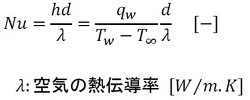外部流れの熱伝達を理解する:CAE解析とExcelを使いながら冷却系設計を自分でやってみる(17)(1/4 ページ)
CAE解析とExcelを使いながら冷却系の設計を“自分でやってみる/できるようになる”ことを目指す連載。連載第17回は、外部流れの熱伝達(自然対流、強制対流)について取り上げる。
ここからは、外部流れの熱伝達について説明します。自然対流熱伝達と強制対流熱伝達がありますが、まずは自然対流から始めましょう。
自然対流熱伝達:水平に置かれた円柱
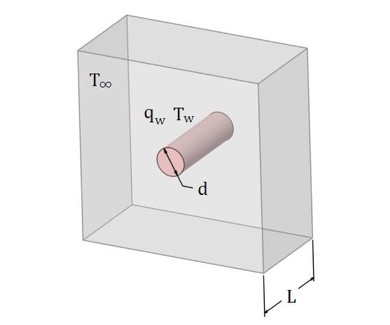
図1に、外部流れと内部流れを示します。これまでは右図の内部流れについて説明してきましたが、今回は左図の外部流れを取り上げます。
熱伝達率を求めるには、まずヌセルト数を求める必要があります。そのためには、グラスホフ数Grとレーレー(またはレイリー)数Raを求めなければなりません。これらの定義は、次式の通りです(参考文献[1])。
水平に置かれた円柱の熱伝達率については、実験結果から導かれた整理式があり、次式のように表されます(参考文献[1])。
この計算は、少し骨が折れますね。一例を紹介します。解析条件を図2に示します。2次元問題ではありますが、設計計算Excelシートを作成する際に必要となるため、奥行き寸法をL[m]としました。円柱の表面温度をTw、主流の温度(室温)をT∞とします。
計算手順は、以下の通りです。
(1) 円柱の発生熱量と表面積から、伝熱界面の熱流束を求める。
(2) 空気の主流の温度におけるプラントル数、動粘性係数、熱伝導率、体積膨張係数を求める。
(3) (Tw−T∞)を未知数とするが、取りあえず仮の数値を決めておく。
(4) 式5を用いてヌセルト数を計算する。
(5) 式4に含まれるプラントル数の関数C1を計算する。
(6) グラスホフ数とレーレー数を求める。
(7) 式3からnを計算する。
(8) Excelで以下の値を計算する。なお、レーレー数によって使用する式が異なる。
(9) Excelのゴールシーク機能を使って、(8)で計算された値がゼロとなるような未知数(Tw−T∞)を求める。この時点で、伝熱界面温度Twが求まっている。
(10) 式5を用いて、熱伝達率hを求める。
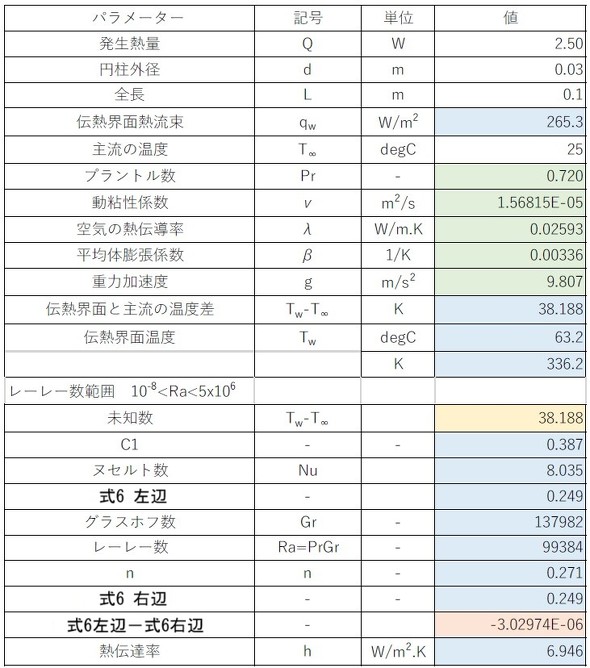
表1に、自然対流熱伝達における熱伝達率の計算例を示します。
これまで紹介してきた計算式は、水平に置かれた円柱に適用されるものです。世の中には、直方体や多面体など、さまざまな形状の物体がありますが、それらの熱伝達率を求める式はなかなか見つかりません。
空気の場合、いろいろな形の自然対流熱伝達では、熱伝達率を2〜3[W/(m2.K)]として大まかに見積もることになります。ちなみに、鉄鋼材料の金属疲労で使用する下限界応力拡大係数も、2〜3[MPa√m]と覚えやすい値です。
Copyright © ITmedia, Inc. All Rights Reserved.