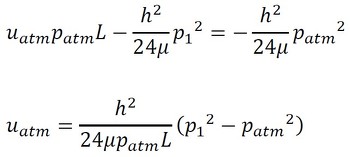圧縮性流体の圧力損失を求めて実験値と比較する：CAE解析とExcelを使いながら冷却系設計を自分でやってみる（11）（5/5 ページ）

CAE解析とExcelを使いながら冷却系の設計を“自分でやってみる／できるようになる”ことを目指す連載。連載第11では、マッハ数が0.003［-］という実験値を基に、層流における圧縮流体の圧力損失を求め、その結果を実験値と比較する。

[高橋良一／ＲＴデザインラボ 代表，MONOist]

　変数分離形になったので、両辺を積分します（式26）。

式26

　積分定数を求めるための境界条件として、上流（x＝0とします）での圧力をp₁としましょう。式27、式28の関係となります。

式27

式28

　これらを式26に代入します（式29）。

式29

　出口での流速はu_atmです。x＝L、p＝p_atmを代入すると、式30になります。

式30

　ここから、流量は式31となります。

式31

　なお、流量計を通過しているガスの圧力が高く、温度も0［℃］でない場合、ガス流量計は通常、圧力が大気圧、温度が0［℃］になったと仮定したときの流量を出力します。単位は［Nm³/h］で、「毎時ノルマルリューベ」と呼ばれます。

　今回の問題では出口が大気開放されているので、圧力に関してはそのままの値を使うことができますが、温度については補正が必要になります。

圧縮性流体の圧力損失　実験値との比較

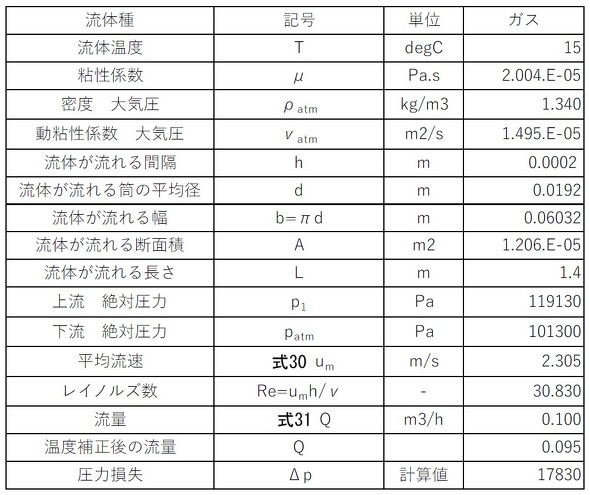
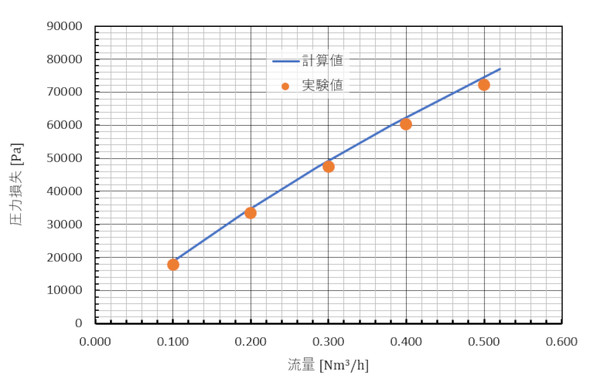
　いよいよ実験値との比較です。表2に計算結果を、図6に圧力損失の実験値と計算値を示します。両者は良い一致を示しました。

表2　圧縮性流体の圧力損失の計算例［クリックで拡大］

図6　圧力損失［クリックで拡大］

　グラフを見ると、流量が0.5［Nm³/h］のとき、圧力損失は7万［Pa］であり、大気圧（10万1325［Pa］）の約0.7倍に相当します。従って、このときの上流側の絶対圧は約17万3500［Pa］、つまり大気圧の1.7倍です。入り口と出口の圧力比が1.7［-］なので、流速比は1／1.7［-］となり、出口の流速は入り口の1.7倍になります。つまり、入り口側の気体はかなり圧縮されていることになります。

---

　層流の話はこのあたりにしておきましょう。次回からは乱流に入ります。かなり手ごわいですよ。　（次回へ続く）

⇒「連載バックナンバー」はこちら

Profile

高橋 良一（たかはし りょういち）
ＲＴデザインラボ 代表

1961年生まれ。技術士（機械部門）、計算力学技術者 上級アナリスト、米MIT Francis Bitter Magnet Laboratory 元研究員。

構造・熱流体系のCAE専門家と機械設計者の両面を持つエンジニア。約40年間、大手電機メーカーにて医用画像診断装置（MRI装置）の電磁振動・騒音の解析、測定、低減設計、二次電池製造ラインの静音化、液晶パネル製造装置の設計、CTスキャナー用X線発生管の設計、超音波溶接機の振動解析と疲労寿命予測、超電導磁石の電磁振動に対する疲労強度評価、メカトロニクス機器の数値シミュレーションの実用化などに従事。現在ＲＴデザインラボにて、受託CAE解析、設計者解析の導入コンサルティングを手掛けている。⇒ ＲＴデザインラボ