使わなければ話にならない「接触要素」(その2):CAEを正しく使い疲労強度計算と有機的につなげる(13)(1/4 ページ)
金属疲労を起こした際にかかる対策コストは膨大なものになる。連載「CAEを正しく使い疲労強度計算と有機的につなげる」では、CAEを正しく使いこなし、その解析結果から疲労破壊の有無を予測するアプローチを解説する。連載第13回は、前回に引き続き「接触要素」について取り上げる。
連載第12回では、機械の結合部品、ボルト、溶接部で疲労破断がよく発生し、これらを未然に防止するには部品間に接触要素を配置し、部品同士の接触と分離をシミュレートする必要があると述べました。
ほとんどのCAEソフトには接触解析機能がありますが、今回はどのような接触状態が解析できれば実務に耐えられるのかを、解析事例を使って説明します。また、接触要素を使うと計算が収束せず、解析が途中で停止することがよくありますが、この防止テクニックについても触れます。
連載第1回の問題の解決
図1に、連載第1回の解析結果を示します。ボルトに大きな曲げ応力が発生したことが問題でした。連載第1回の解析条件は適切なものではなかったようです。これから述べる解析方法が理想的かどうかは自信がありませんが、「筆者ならこのようにする」と考えられる方法を紹介します。
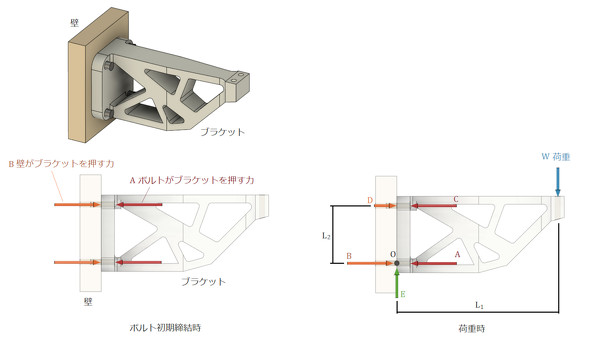
ブラケットに作用する力のつり合いをもう一度考えてみましょう。図2のような力のつり合い図を描いてみました。
まず、図2下部の左図のボルト初期締結時に注目します。ボルトの締結力によってボルトがブラケットを押す力Aと、この反力である壁がブラケットを押す力Bがあります。ブラケットの自重は考えないことにします。次に、図2下部の右図の荷重時に注目します。先ほどのブラケットを押す力Aはほとんど変わらず、少しだけ増えてCとなり、ブラケットを押す力Bがかなり小さくなってDとなります。
O点周りのモーメントのつり合い式を以下のように作ることができます(式1)。
式1: −L1W+L2C−L2D=0
荷重WによってAは大きくなるのですが、ボルトが締結されている場合、その増加量は直観的に見積もられる増加量に内力係数φを掛けた値となり、φは0.15[-]程度の値です。この理由から、Aはほとんど変わりません。荷重Wに拮抗(きっこう)する力は、Dが小さくなった分になります。内力係数φについては、本連載後半で取り上げるボルトの解説のところで説明します。力Eは荷重Wと同じ値です。B+Dに、摩擦係数を掛けた値がWを下回ったとき、ブラケットがずれ落ちて図1のような状態となりますが、ボルトの締結力は大きいのでずれ落ちることはありません。
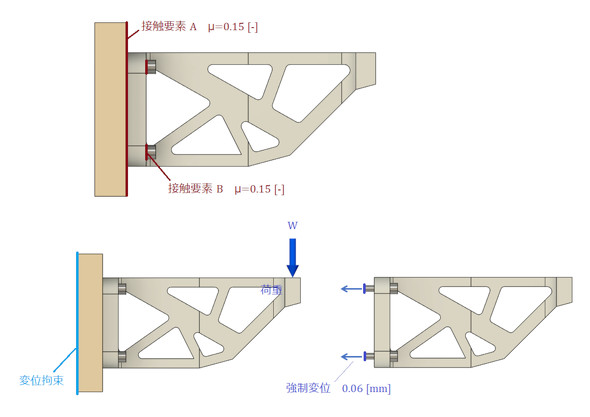
では、ボルトの初期締結力を考慮して解析してみましょう。図3に、解析モデルと境界条件を示します。
ボルトの底に強制変位を掛けることでボルトの初期締結力を生成させます。3回ほど解析を繰り返して式2が成立するような強制変位量を見つけることになります。ボルトプリテンション機能がある有限要素法ソフトならば、所望の締結力を簡単に発生させることができます。
式2: ボルトの初期締結力=ボルトの軸方向応力平均値×ボルトの断面積
ボルトの底に初期締結力の荷重を掛けても似たような解析結果が得られますが、これだと荷重Wによるボルトの応力増加量を求めることができません。このボルト応力増加量の半分が、ボルトに発生する応力振幅でボルトの疲労破断の有無を予測するのに必要な応力となります。この辺も本連載の後半で説明します。
図3の接触要素Bは少しやり過ぎですね。解析結果の見栄えのためにこのようにしました。固着の接触要素でよいと思います。
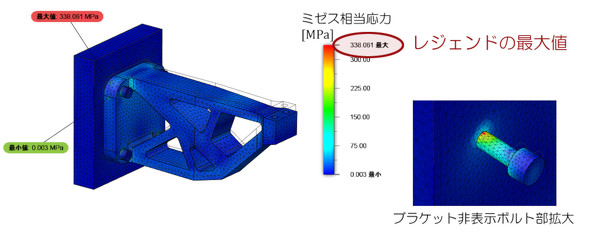
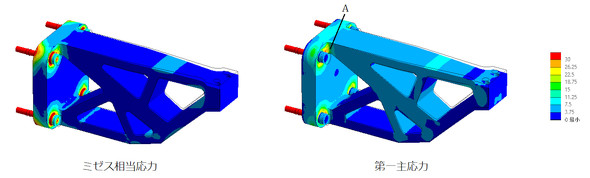
図4に、解析結果を示します。
図4左図は、ミゼス相当応力です。ボルトの頭に応力の高い領域(赤色領域)があります。ミゼス相当応力は引張応力が大きいところと、圧縮応力が大きいところの両方で高応力領域となるので、このような結果となりました。関心事は引張応力なので、第一主応力を見ましょう。図4右図は第一主応力分部ですが、ボルト頭部の赤色はなくなりました。ボルト頭部には圧縮応力が作用していました。第一主応力を見る限り、A部の応力をチェックしておけばよいようです。
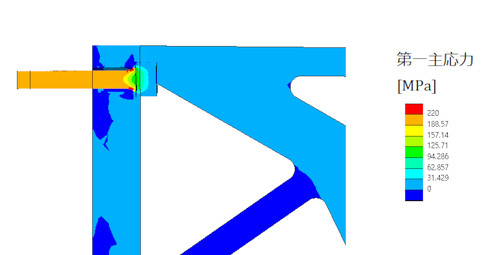
図5に、ボルト断面の第一主応力分布を示します。
ボルトには一様な引張応力が発生し、降伏応力の70[%]くらいです。というか、降伏応力の70[%]くらいになるように強制変位量を設定しました。荷重ありと荷重なしのボルト軸部の応力を読み取り、その差の2分の1が応力振幅となり、これとボルトの疲労強度とを比較してボルトの疲労破断の有無を予測します。
Copyright © ITmedia, Inc. All Rights Reserved.