「安全率」について考える：CAEを正しく使い疲労強度計算と有機的につなげる（9）（3/4 ページ）

金属疲労を起こした際にかかる対策コストは膨大なものになる。連載「CAEを正しく使い疲労強度計算と有機的につなげる」では、CAEを正しく使いこなし、その解析結果から疲労破壊の有無を予測するアプローチを解説する。連載第9回では、いよいよ「安全率」の話題に突入する。

[高橋良一／ＲＴデザインラボ 代表，MONOist]

角Rがゼロのときの切欠係数βの確認作業

　角Rがゼロのときの切欠係数が分かりました。では、ウラを取りましょう。日本機械学会では、過去に報告された切欠係数の値を集めた散布図を作りました。これもその図をそのまま転載するわけにはいかないので筆者が作りました。図7に示します。

図7　切欠係数βの分布 鉄鋼材料（参考文献［2］）［クリックで拡大］

　黒色の丸プロットがあるということは、そのようなデータが得られた実験があったということです。よく見るとβ＞3.5［-］のプロットが見当たりません。つまり、そのような実験データがないということです。実験の中には応力集中の激しいものがあったと推測されますが、切欠係数の上限は3.5［-］くらいのようです。図7は文献を見て作ったものなので、確認する場合は参考文献［2］を参照ください。若いころ、「高橋君、応力集中のところは3でいいんだよ」と言ってくれた先輩の助言は、全然的外れではなかったのです。

　切欠係数βは3くらいだと分かりました。そして、必要なのは応力集中部の応力ではなく、応力集中成分を除いた「公称応力」だということも述べました。では、CAE解析なんかやらずに、はりの計算をやっていればよいのでしょうか。

参考文献：

• ［2］日本機械学会｜金属材料 疲労強度の設計資料 I（1991）

不静定問題が得意な有限要素法

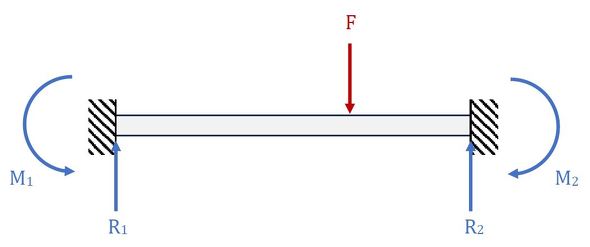
　CAE解析不要論的なことを述べましたが、CAE解析が必要な場面を紹介します。図8のはりのたわみと応力を求める問題を考えます。

図8　はりのたわみと応力を求める問題［クリックで拡大］

　固定端の反力R₁、R₂とモーメントM₁、M₂は未知数になるので、4つの条件、例えば左端の変位と傾きがゼロ、荷重点の変位と傾きが連続などの条件から4つの式を作って未知数を求めます。このような問題を「不静定問題」といいます。では、やってみましょう。図9です。

図9　不静定はりの計算［クリックで拡大］

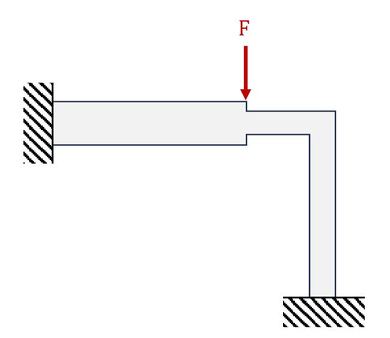
　実はこれ、計算間違い探しの時間を加えると約半日かかりました……。では、図10のような問題はどうでしょうか。戦意が消失しますね。有限要素法ソフトは不静定問題も得意なので、文句を言わずに計算してくれます。CAE解析の出番はいくらでもあると思います。

図10　はりのたわみと応力を求める問題［クリックで拡大］

角Rがゼロの段付きはり

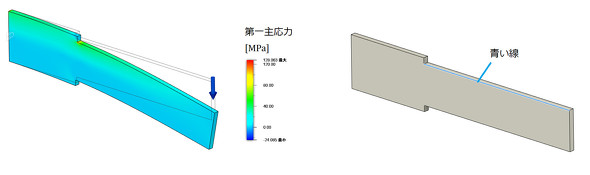
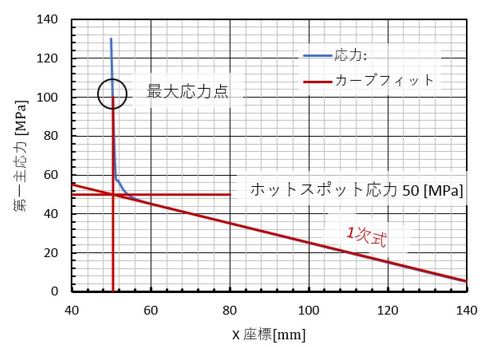
　最後に、角Rがゼロの段付きはりの強度計算をしましょう。連載第5回でシャフトの角Rを0.5［mm］としましたが、それよりもはるかに小さなRで製作されることはよくあります。また、「解析用モデル」といって製作用3Dモデルを簡素化し、C面取りや角Rが除去されたモデルを作ってCAE解析をすることがあります。図11に角Rがゼロのときの応力分布を示します。そして、青色の線上にある節点の応力から「ホットスポット応力」を求めます。これを図12に示します。

図11　角Rがゼロのときの応力分布［クリックで拡大］

図12　青色の線上にある節点の応力とホットスポット応力［クリックで拡大］

　連載第8回と全く同じ結果となりました。角Rが小さい場合は、解析モデルの角Rをゼロに変更、つまりフィレットを削除してCAE解析すればよいと思います。そして、ポットスポット応力と疲労強度をβで除した値を比較します。こうすれば節点数と要素数が減り、計算時間も短縮できます。