1次要素と2次要素は「次元が違うくらい」異なる!?:CAEを正しく使い疲労強度計算と有機的につなげる(5)(1/4 ページ)
金属疲労を起こした際にかかる対策コストは膨大なものになる。連載「CAEを正しく使い疲労強度計算と有機的につなげる」では、CAEを正しく使いこなし、その解析結果から疲労破壊の有無を予測するアプローチを解説する。連載第5回は「1次要素」と「2次要素」について取り上げる。
今回は「1次要素」と「2次要素」の説明をして、「1次要素は今後一切使わず、2次要素を使いましょう」という内容をご紹介します。
要素の種類
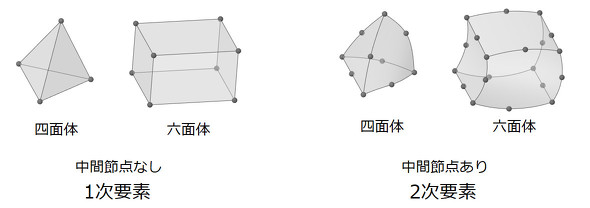
「有限要素法」で選択できる要素を図1に示します。通常は「四面体要素」を使うことになります。というのは、任意の形状の3D CADモデルを要素分割できるのは四面体要素だけのようです。任意の形状のモデルを「六面体要素」で分割するアルゴリズムはまだ見つかっていません。
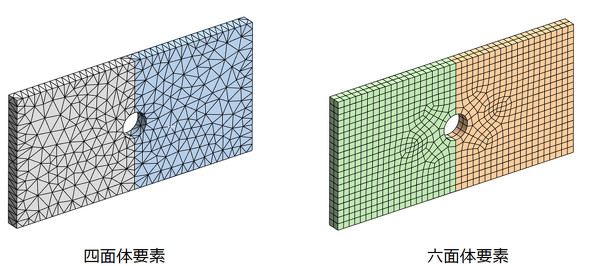
図2に四面体要素で要素分割した例と、六面体要素で要素分割した例を示します。任意の形状の2次元平面を四角形で要素分割できるアルゴリズムはあるので、図2右図のように、正面の面を四角形で要素分割して、それを奥行き方向に掃引すると六面体要素で要素分割できたことになります。
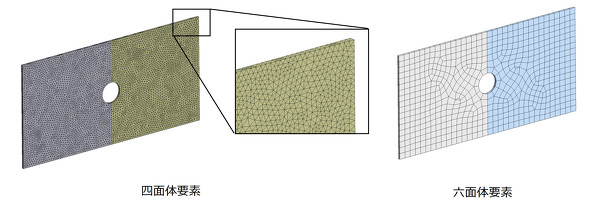
図3に薄い板を要素分割した例を示します。この場合、いくつかのメッシャーでは四面体要素で要素分割すると要素数が爆発的に増えてしまいます。六面体2次要素であれば、薄い要素、つまりアスペクト比が大きな要素でも、2次要素なら解析精度があまり落ちないので要素数を劇的に少なくできます。
さらに、「ピラミッド要素」というものがあり、四面体要素と六面体要素を節点結合させる際に必要になります。他にも「三角柱要素」というものもあり、図2右図のように、正面の面がたまたま三角形で要素分割されたときに出現します。
1次要素の中の応力分布
有限要素法で応力解析したときの、要素内の応力分布の仕方について述べます。前回、2次元平面応力問題の要素剛性マトリクスは次式で求められることを説明しました。
[B]は変位ひずみマトリクスでした。変位ひずみマトリクスを作るときに要素内の変位を次式で仮定しました。要素内の変位は座標の1次式で補間されます。
α1、α2、β1、β2は節点座標だけで決まります。つまり、定数です。そして、ひずみは変位を座標x、yで偏微分すれば求まるとも述べました。
では、式2をxで偏微分しましょう。次式です。
同様の計算をすると、εx、εy、γxyはα1、α2、β1、β2で決まり、それらは定数です。応力は次式で表した応力−ひずみマトリクス[D]とひずみベクトルとの積で、応力−ひずみマトリクス[D]はヤング率とポアソン比だけで決まります。この結果、要素内で応力は座標に関係なく一定値となります。
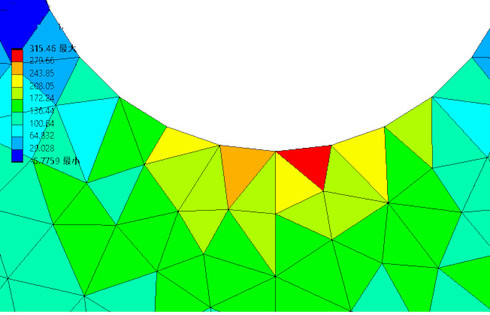
1次要素では要素内の応力とひずみが一定値なので、図示すると図4となります。「この驚愕の事実、こんなにラフな計算だったのか」と思われたかもしれませんが、その理由は前述した通りです。といっても、初めて有限要素法を知ったときは、要素内応力が一定であっても弾性力学の式の解が求まるのなら大歓迎だったのです。
2次要素の中の応力分布
2次要素では変位の補間が2次式ということで、形状関数が2次式です。変位の補間式は次式となります。
では、式7をxで偏微分しましょう。次式です。
ひずみは要素内で1次式に従って変化します。よって、応力も1次式で変化します。図5に2次要素を使ったときの応力分布を示します。なかなかイイ線いってますね。
Copyright © ITmedia, Inc. All Rights Reserved.