「安全率」について考える:CAEを正しく使い疲労強度計算と有機的につなげる(9)(2/4 ページ)
金属疲労を起こした際にかかる対策コストは膨大なものになる。連載「CAEを正しく使い疲労強度計算と有機的につなげる」では、CAEを正しく使いこなし、その解析結果から疲労破壊の有無を予測するアプローチを解説する。連載第9回では、いよいよ「安全率」の話題に突入する。
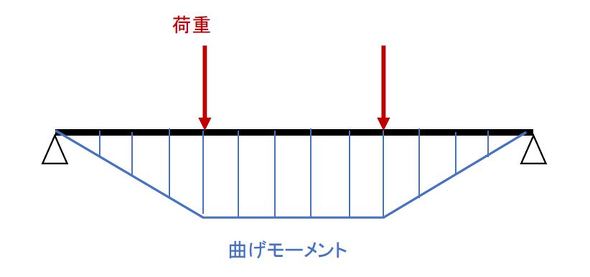
では先に、「小野式回転曲げ疲労試験機」について説明します。これは材料の疲労強度を簡単に測定できる機械です。図3に荷重箇所が2つある両持ちはりを示します。曲げモーメント図から、中央部分の曲げモーメントは位置によらず一定値となります。
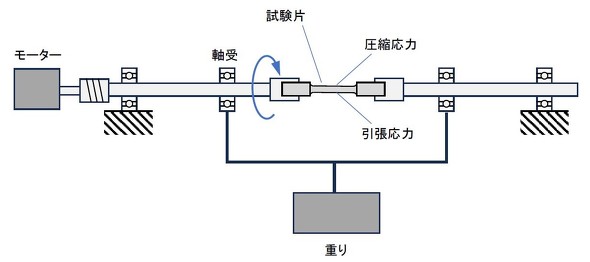
図4に、小野式回転曲げ疲労試験機を示します。おもりによって試験片には一定の曲げ応力が作用し、試験片の上側には圧縮応力が、下側には引張応力が発生します。そして、この試験片を回転させると試験片には圧縮応力と引張応力が交互に発生して、総回転数が荷重回数となります。
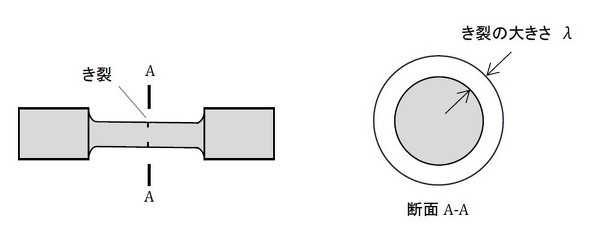
参考文献[1]を紹介します。ここにはき裂、つまり角Rがゼロのときの疲労強度を実験で求めたことが書かれています。どのように試験をしたかというと、まず少し重めのおもりを装着して試験をし、試験片に図5に示すようなき裂を発生させます。このとき、き裂先端の角Rはゼロですね。ここまでは準備段階です。
き裂の大きさλが0〜3.0[mm]の試験片を作って、これらの試験片を使って疲労試験をし、破断した回数とそのときのおもりの質量を記録します。おもりの質量から曲げ応力が求まります。断面二次モーメントは図4の着色した断面の直径から求めたとのことです。表1に試験片の材質を示します。文献の応力の単位は[kgf/mm2]だったので[MPa]に変換してあります。SF-60は引張強さが60[kgf/mm2]級の鋼です。
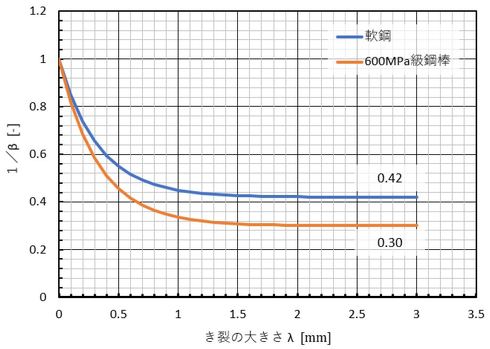
図6に試験結果を示します。これも文献の図をそのまま転載できないので筆者が作りました。縦軸は切欠係数βの逆数です。き裂の切欠係数βは、引張強さが400[MPa]級の鉄鋼では1/β=0.42,β=2.4[-]、600MPa級鋼棒では1/β=0.30,β=3.3[-]となります。この数値は覚えておいて損はないと思います。
Copyright © ITmedia, Inc. All Rights Reserved.