「安全率」について考える：CAEを正しく使い疲労強度計算と有機的につなげる（9）（1/4 ページ）

金属疲労を起こした際にかかる対策コストは膨大なものになる。連載「CAEを正しく使い疲労強度計算と有機的につなげる」では、CAEを正しく使いこなし、その解析結果から疲労破壊の有無を予測するアプローチを解説する。連載第9回では、いよいよ「安全率」の話題に突入する。

[高橋良一／ＲＴデザインラボ 代表，MONOist]

　いよいよ「安全率」についてウンチクを述べる段階まで来ましたが、あと少しだけ「切欠係数」のお話にお付き合いください。

⇒「連載バックナンバー」はこちら

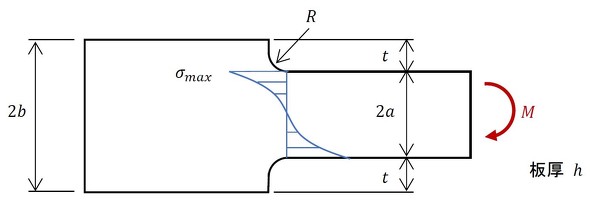
角Rがゼロのときの切欠係数βはいくらか？

　連載第6回の角Rがある事例（段付き板の曲げ問題）を図1に再掲します。角Rがゼロのときの応力集中係数αは無限大です。角Rがゼロのときの切欠係数βはいくらでしょうか。破壊力学の出番なのでしょうか。

式1

図1　角R問題 2次元版（段付き板の曲げ問題）［クリックで拡大］

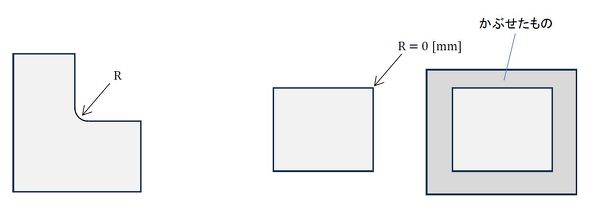
　図2に機械加工した部品の形状を示します。

図2　機械加工した部品の形状［クリックで拡大］

　旋盤やフライス盤で加工した場合は、工具（カッター）の先端の曲率半径はゼロではありません。もし、ゼロだったら工具の先端はすぐに摩耗して小さなRができます。ということは、図2左側のように凹状部のRはゼロになりません。しかし、包丁の刃を考えれば右側のように凸状部のRはゼロにできます。この部品に何かを被せたとします。被せたものの凹状部のRはゼロになりますね。中身の部品と被せたものの線膨張率やヤング率が異なっていたら、R部の応力集中係数は無限大となります。このような例として、樹脂モールド品や鋼で作った埋金を入れたアルミ鋳物などがあります。あまり付加価値の高い部品ではないのでCAE解析の出番にならないかもしれませんね。

　き裂の角Rはゼロなので破壊力学の出番です。筆者が会社勤めをしていたときに研究成果のポスター発表会があり、そこで「J積分」の事例が公開されていました。J積分と応力拡大係数には密接な関係があり、J積分値が大きければ応力拡大係数も大きくなります。話を伺うと半導体関係の仕事だそうで、いくつかの設計案のJ積分値を比較して、値が小さいものを選んでいるとのことでした。

　ここからは筆者の想像ですが、半導体の生産は常に歩留り向上が要求されます。1枚のウエハーからチップが100個取れるとしましょう。出来上がったチップを試験して正常に動作したものが30個だとしたら、歩留まりは30［％］となります。ゲーム機が発売当初に品薄になるのは歩留まりが思ったほど向上しなかったためと推測しています。その後、歩留まりが上がって十分な量が供給されるようになります。たくさんの設計案やプロセス条件案があったとき、全て実験すればよいのですが、最近の半導体はウエハーを投入してから出来上がるまで3カ月以上要すると聞いています。あまりたくさんの試験ができないので、例えばJ積分値を比較して設計案の絞り込みをすることは有効な手段となります。これなら、かなり付加価値の高い仕事になり、CAE解析の出番となります。

　少し脱線しました。角Rがゼロの製品はいろいろとあるので、角Rがゼロの切欠係数βは知りたいものです。いずれにしてもこの値を知っておけば、応力集中部の応力を求める必要はなくなりますね。