応力集中があるときの金属の疲労強度：CAEを正しく使い疲労強度計算と有機的につなげる（8）（1/4 ページ）

金属疲労を起こした際にかかる対策コストは膨大なものになる。連載「CAEを正しく使い疲労強度計算と有機的につなげる」では、CAEを正しく使いこなし、その解析結果から疲労破壊の有無を予測するアプローチを解説する。連載第8回は、前回に引き続き「金属疲労のおさらい」的な内容をお届けする。

[高橋良一／ＲＴデザインラボ 代表，MONOist]

　応力集中があるときの金属の疲労強度は切欠係数βを使うことになっていましたね。前回に引き続き、今回も「金属疲労のおさらい」的な内容となります。

⇒「連載バックナンバー」はこちら

応力集中係数αと切欠係数βは同じ値か？

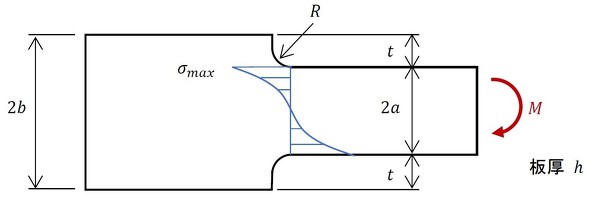
　連載第6回の角Rがある事例（段付き板の曲げ問題）を図1に再掲します。応力集中係数は弾性力学の範囲、つまり塑性変形がない状態で弾性力学の方程式を解くことで求められます。有限要素法が普及する前は光弾性実験などで求めていました。段付き板の曲げ問題において、応力集中部の最大応力は式1で求めることができます。

図1　角R問題 2次元版（段付き板の曲げ問題）［クリックで拡大］

式1

　切欠係数の定義を式2に示します。

式2

　切欠係数は実験で求まります。というか、実験でしか求めることができません。図1の場合、応力集中が発生していないときの応力は、基準応力σ_oに相当し、「応力集中のない部材の疲労強度」は幅2aの板を曲げ試験して求めます。そして、切欠係数βは図1の状態で曲げ試験を行い、「応力集中が発生している部材の疲労強度」を求め、これら2つの疲労強度から算出できます。

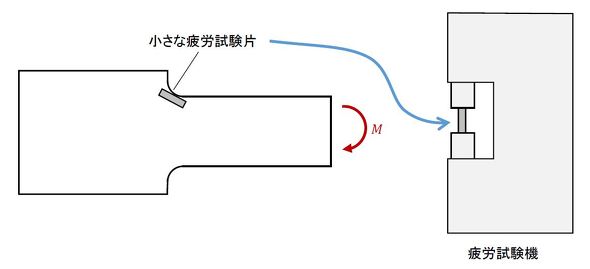
　では、図2のようなケースを考えます。応力集中を起す部品の応力集中部から小さな疲労試験片を取り出して、それを疲労試験機にかけるとどうなるでしょうか。

図2　小さな疲労試験片の疲労試験［クリックで拡大］

　「これいかに？」といった感じで禅問答のようになりました。疲労試験機が発生する応力は応力集中部の応力であって、このときの疲労強度が求まるはずです。ということは、応力集中係数αと切欠係数βは一致することになるのでしょうか。実は「一致しない」という実験結果があります。図3に応力集中係数αと切欠係数βの関係を示します。参考文献［1］の図をそのまま掲載するわけにはいかないので、この図は筆者が作りました。

図3　応力集中係数αと切欠係数βの関係（参考文献［1］）［クリックで拡大］

　SS400のような軟鋼の場合は、αが2以下でαとβが一致しますが、それ以上ではαがいくら大きくなってもβは頭打ちとなって2［-］くらいです。焼き入れ鋼のように合金鋼ではαが3.5［-］以上で頭打ちとなります。応力集中が激しい場合は、応力集中係数αと切欠係数βは一致しません。あと一つ、引張強さが大きくなるとβが大きくなることにも注目してください。

参考文献：

• ［1］石橋｜金属の疲労と破壊の防止｜養賢堂（1967）