応力集中があるときの金属の疲労強度：CAEを正しく使い疲労強度計算と有機的につなげる（8）（3/4 ページ）

金属疲労を起こした際にかかる対策コストは膨大なものになる。連載「CAEを正しく使い疲労強度計算と有機的につなげる」では、CAEを正しく使いこなし、その解析結果から疲労破壊の有無を予測するアプローチを解説する。連載第8回は、前回に引き続き「金属疲労のおさらい」的な内容をお届けする。

[高橋良一／ＲＴデザインラボ 代表，MONOist]

応力集中を小さくしたけれど……

　「CAE解析結果を使うと過剰品質になる」と書きましたが、部品が壊れるわけではないので別に問題はありません。ただ、次のような場合には注意が必要です。

　今の時代、疲労破壊問題が発生するとほとんどの場合、CAE解析を行うでしょう。そして、応力集中部の応力が求まります。ここで、角Rを大きくして、例えば最大応力が350［MPa］から210［MPa］になったとします。応力集中係数αは5［-］から3［-］になりました。応力は60［％］まで低減しました。これで改善されるのでしょうか。

　図3の軟鋼の場合、切欠係数は両者2.4［-］なので、応力は60［％］まで低減しましたが、同様に疲労破断するとの予測となりました。このような事例を筆者は経験したことがありません。しかし、図3をよく見てみると、このようなこともあり得るのではないかと思いました。

ホットスポット応力

　CAE解析結果が疲労破壊の有無に使えない状態となりました。何とかしましょう。基準応力は応力集中成分を含まない応力なので「公称応力」と呼ばれています。これに対し、応力集中成分を含む応力は単に「応力」といいますが、違いを強調するために、ここでは「真応力」と呼んでいます。前回の真破断力と異なることに注意してください。公称応力をCAE解析結果から求める方法を説明します。

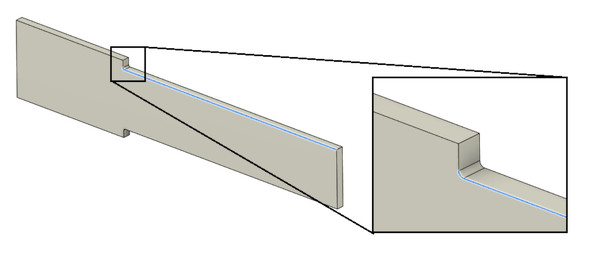
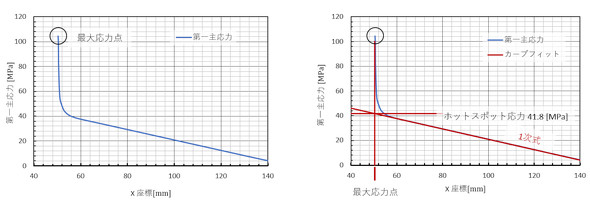
　図7の青色の線上にある節点の第一主応力を、グラフにしたものを図8に示します。

図7　応力抽出位置［クリックで拡大］

図8　第一主応力の分布［クリックで拡大］

　図8において、X座標が60〜140［mm］のところの応力を1次式でカーブフィットして、その1次式を延長します。図8右図の赤色線でこれを示します。一次式は次式ですね。a、bはカーブフィットして求めます。Excelの「近似曲線の追加」機能でできます。

式12

　次に、最大応力点のX座標x_{σ max}を求め、これを式12に代入したものが「ホットスポット応力」（参考文献［3］）と呼ばれるものです。式13となります。

式13

　ホットスポット応力は41.8［MPa］と式5と一致し、ホットスポット応力を公称応力と使ってよさそうです。

　前述した例では、片持ちはりの応力なので応力の変化は1次式だったのですが、応力の変化が1次式でない場合や、ひずみゲージを使って実験的に応力を求めるときは指針があります。

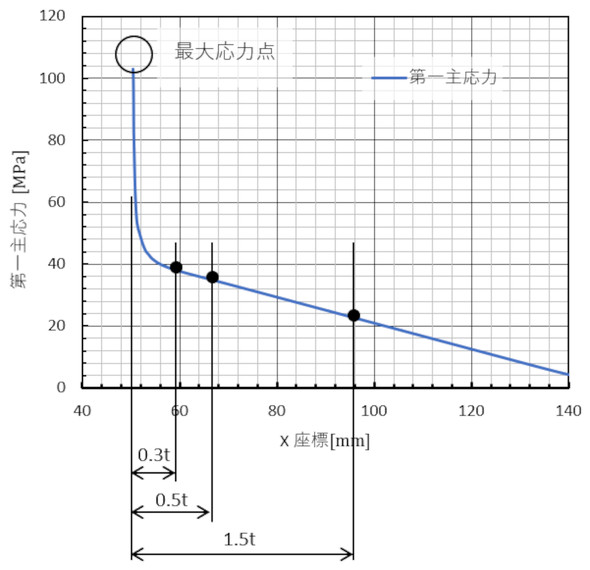
　1つ目は、最大応力点から板厚の0.3倍の位置の応力をホットスポット応力とします。2つ目は、板厚の0.5倍の位置の応力と1.5倍の位置の応力を直線で結び、最大応力点に外挿した応力値です。溶接の場合の最大応力点は溶接止端位置となります。この指針は他の文献では異なる数値となりますが、応力分布をカーブフィットするという考え方でよいと思います。

　図9のtは図4におけるh＝3.6［mm］ではなく、図4の26［mm］と書いてある寸法のことです。板厚の0.3倍の位置の応力は溶接構造物などの板厚が薄いときに有効になります。

図9　ホットスポット応力を決めるときの応力読み取り位置［クリックで拡大］

　図4の段付きはりの疲労強度計算では、公称応力をホットスポット応力σ_HSで代用し、式14で安全率を求めることになり、手計算と同じ結果となります。

式14

　式14において、切欠係数βは最大応力σ_maxの関数であると表記しました。これはσ_maxから応力集中係数αを求めて、図3から切欠係数βを求めるということですが少々面倒ですね。SS400ならβ＝2.4［-］でいいのではないでしょうか。

参考文献：

• ［3］一般社団法人 日本溶接協会Webサイト｜ホットスポット応力