応力集中があるときの金属の疲労強度:CAEを正しく使い疲労強度計算と有機的につなげる(8)(2/4 ページ)
金属疲労を起こした際にかかる対策コストは膨大なものになる。連載「CAEを正しく使い疲労強度計算と有機的につなげる」では、CAEを正しく使いこなし、その解析結果から疲労破壊の有無を予測するアプローチを解説する。連載第8回は、前回に引き続き「金属疲労のおさらい」的な内容をお届けする。
強度計算例:疲労破壊の有無の予測
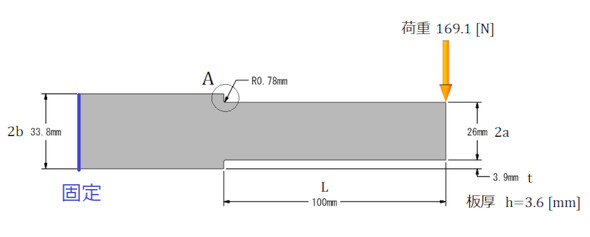
簡単な例で疲労破壊の有無を予測しましょう。図4に示したSS400材でできた段付きはりのA部について、疲労破壊の有無を予測します。
まずは手計算です。参考文献[2]から応力集中係数αは3[-]くらいです。では、基準応力を計算します。次式となります。
基準応力に応力集中係数を掛けると応力集中部の最大応力となり、式6です。
図3から、切欠係数は2.4[-]となります。材料の疲労強度は連載第7回の図6から次式となります。
応力集中部の疲労強度は、切欠係数βの定義から次式となります。
安全率はというと、式9となります。分子の疲労強度は式8の応力集中を持つ部材の疲労強度であって、材料の疲労強度を切欠係数βで割った値です。応力集中による疲労強度低下を織り込んでいるので、式9の分母ははりの計算による値、つまり応力集中による応力増加分を含んでいない値です。
疲労強度と等しい応力振幅が作用したときの破壊確率は50[%]くらいです。マージンは2倍以上ほしいので、このくらいでOKですね。
次に、CAEソフトで強度計算をやってみます。図5に応力分布を示します。
最大応力が128[MPa]となり、式6とほぼ一致しました。つまり、基準応力に応力集中係数を掛けた値と一致しました。安全率は式10となります。
安全率が少し足りませんね。板厚を3.6[mm]から4.5[mm]に変えましょう。図6に解析結果を示します。
最大応力が102[MPa]なので安全率は式11となります。分子の疲労強度は式7の材料の疲労強度で、応力集中による疲労強度低下を織り込んでいません。式11の分母はCAEソフトが出力する応力、つまり応力集中による応力増加分を含んでいる値です。
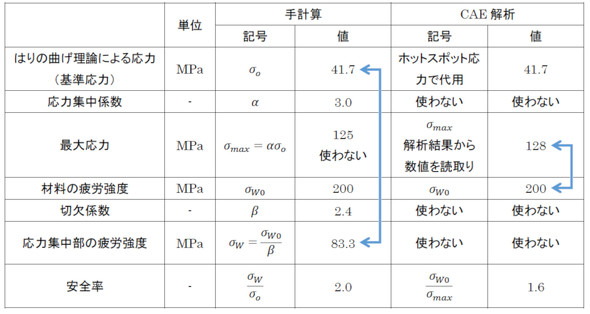
式9と式11では、疲労強度に対する安全率がともに2.0[-]となりましたが、板厚が3.6[mm]と4.5[mm]というように、CAE解析結果に従うと部品の材料費が高くなってしまいました。不経済な設計となります。整理しましょう。表1に手計算による方法とCAE解析による方法を示します。
手計算の安全率の分母、つまり式9の分母は「はりの曲げ理論による応力」で、応力集中成分を含まない応力です。手計算の安全率の分子は応力集中部の疲労強度で、これは切欠係数βで割っているため、応力集中による強度低下分を織り込んだ値です。応力集中による強度低下分を織り込んだ値を使っているので、比較する相手は応力集中成分を含まない応力でよかったのです。
CAE解析の安全率の分母、つまり式11の分母は、CAE解析結果の最大応力で応力集中成分を含んでいます。CAE解析の安全率の分子は材料の疲労強度で、これは応力集中による強度低下分を織り込んでいません。
筆者はどちらを支持するかというと、手計算の安全率です。これは手計算の結果を採用すると材料費が安いからではなく、切欠係数の定義に従っているからです。切欠係数は多くのデータが過去から積み上げられてきたものであり信用できます。
表1の最大応力の行に注目してください。手計算の最大応力は基準応力に応力集中係数を掛けた値で125[MPa]、CAE解析の最大応力は解析結果で128[MPa]と手計算とほぼ一致しています。手計算とCAE解析で安全率が異なった理由は、CAE解析で切欠係数βを使うべきだったところ、応力集中係数αを結果的に使っていたためです。手計算とCAE解析で最大応力がほぼ同じとなりますが、安全率を計算するときに使った数値が異なるのです。仮に、手計算の切欠係数を3.0[-]とすると両者の安全率は等しくなります。
この章のまとめは以下です。
- 応力集中係数αと切欠係数βは異なる値である
- CAE解析結果の最大応力と材料の疲労強度を比較するような強度評価手法は部品コストが上昇する。言い換えると、過剰品質となる
参考文献:
- [2]日本機械学会|機械工学便覧 A4 材料力学(1992)
Copyright © ITmedia, Inc. All Rights Reserved.
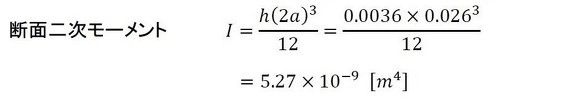
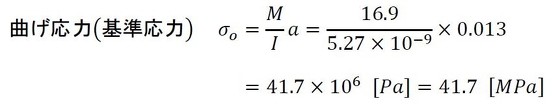
![段付きはりのCAE解析結果 板厚3.6[mm]](https://image.itmedia.co.jp/mn/articles/2407/08/ay4328_caefatigue08_fig05_w590.jpg)
![段付きはりのCAE解析結果 板厚4.5[mm]](https://image.itmedia.co.jp/mn/articles/2407/08/ay4328_caefatigue08_fig06_w590.jpg)