Jetson Orinの生成AI処理性能はXeonの1.7倍、NVIDIAが“史上最大”の機能拡張へ：人工知能ニュース（2/2 ページ）

NVIDIAは、組み込み機器向けのエッジAI開発プラットフォームである「Jetson」について、生成AIへの対応を含めた大幅な機能拡張を行うと発表した。

[朴尚洙，MONOist]

「JetPack 6」は「Ubuntu」などサードパーティー製組み込みLinuxに対応

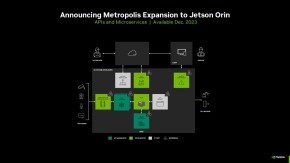
　生成AIへの対応に加えて、JetsonとNVIDIAのAIフレームワークの連携も拡充する。ビジョンAIプラットフォームであるNVIDIA Metropolisとの連携はこれまで限定的だったが、より多くのAPIやマイクロサービスをJetson上で利用できるようになる。JetsonとNVIDIA Metropolisの機能連携は2023年12月のリリースを予定している。

「Jetson」と「NVIDIA Metropolis」の連携機能。従来は限定的だったが（左）、大幅に拡充する（右）［クリックで拡大］ 出所：NVIDIA

　ロボット開発プラットフォームのNVIDIA Isaacについては、オープンソースソフトウェアのロボット開発プラットフォーム「ROS」の開発者向けにAIによる認識機能を容易に実装できるようにする「NVIDIA Isaac ROS」の新バージョンとなる「NVIDIA Isaac ROS 2.0」を投入する。シミュレーション環境の「NVIDIA Isaac SIM」も新バージョンとなる「Isaac Sim 2023.1」を提供する。これらNVIDIA Isaacの新バージョンは2023年10月中にリリースする計画だ。

「NVIDIA Isaac」の機能拡充［クリックで拡大］ 出所：NVIDIA

　開発環境のJetPackの最新版となるJetPack 6は2023年11月にリリースする予定だ。これまでJetPackでは独自のLinuxである「Jetson Linux」が提供されていたが、JetPack 6ではROSベースのロボットで広く利用されている「Ubuntu」の他、「Wind River Linux」「Redhawk Linux」など、サードパーティー製の組み込みLinuxにも対応するようになった。この他にセキュリティ機能なども拡充されている。

「JetPack 6」はこれまでで最大のアップデートとなる［クリックで拡大］ 出所：NVIDIA

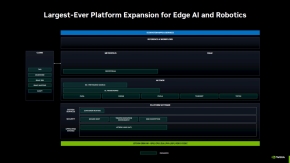
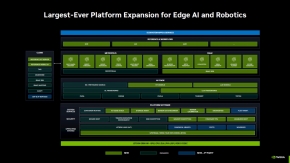
　今回の発表により、Jetsonは大幅な機能拡張を果たすことになる。

これまで「Jetson」で利用可能だった機能（左）。今回の発表は「Jetson」史上最大の機能拡張となる（右）［クリックで拡大］ 出所：NVIDIA

⇒その他の「組み込み開発ニュース」の記事はこちら