FFTアナライザを使いこなそう！：CAEと計測技術を使った振動・騒音対策（6）（1/5 ページ）

“解析専任者に連絡する前に、設計者がやるべきこと”を主眼に、CAEと計測技術を用いた振動・騒音対策の考え方やその手順を解説する連載。連載第6回では、「FFTアナライザ」を使うに当たって最低限知っておくべき内容を取り上げる。

[高橋良一／ＲＴデザインラボ 代表，MONOist]

　振動対策と騒音対策では、横軸を周波数として取り扱うことが常とう手段です。今回は「FFTアナライザ」を使うに当たって“最低限知っておくべきこと”について取り上げます。

⇒「連載バックナンバー」はこちら

トリガ機能の活用

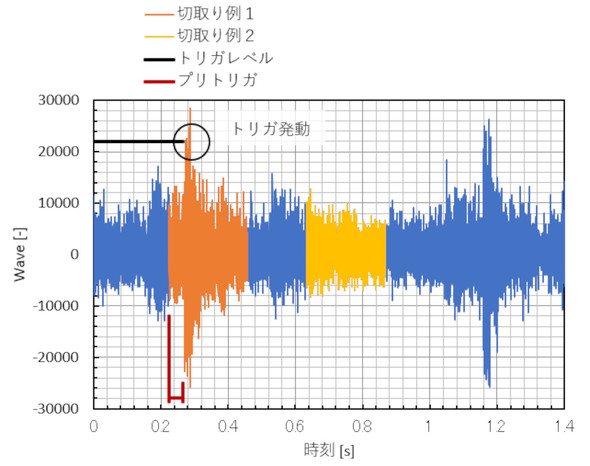
　図1にプレス騒音のデータ切り取り例を示します。連載第5回では、オレンジ色のデータを周波数分析すべきだと述べました。FFTアナライザでこの部分のデータを分析するために「トリガ機能」を使います。振動／騒音対策では、トリガ機能は常に使うと考えた方がいいでしょう。

図1　データの切り取り例［クリックで拡大］

　トリガ機能を使うには、以下の3つの情報をFFTアナライザに教える必要があります。

1. トリガレベル
2. 立ち上がりか、立ち下りか
3. プリトリガ長さ

　信号が「トリガレベル」を超えたときに“トリガ発動”となります。測定波形を見ながら分析したい範囲を決めて、トリガレベルは信号のピーク値の80［％］くらいの値を設定します。

　「立ち上がりか、立ち下りか」は、「立ち上がり」に設定すると信号がトリガレベルを超えたときに“トリガ発動”となり、「立ち下がり」に設定すると信号がトリガレベルより小さくなったときに“トリガ発動”となります。

　「プリトリガ機能」は、分析開始時刻をトリガ発動より「プリトリガ長さ」だけ早い時刻とする機能です。このような設定をして、図1のオレンジ色のデータを分析します。くれぐれも図1の黄色のデータを分析しないように注意してください。

周波数成分のピーク値はそんなに大切なのか？

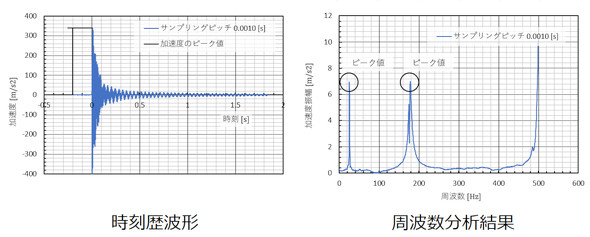
　図2に振動加速度の時刻歴波形と周波数分析結果を示します。振動対策では左側の時刻歴波形のピーク値を小さくしたいのですが、右側の周波数分析結果のピーク値を見て一喜一憂していてよいのでしょうか。よほど測定条件を一致させない限り、周波数分析結果のピーク値を見て一喜一憂するのはやめましょう。それでは間違った判断をしかねません。

図2　振動加速度の時刻歴波形と周波数分析結果［クリックで拡大］

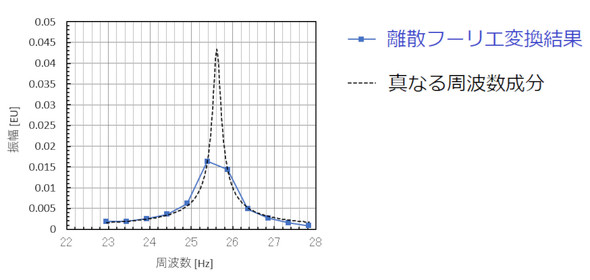
　図3は周波数分析結果と真なる周波数成分を示します。「離散フーリエ変換」なので、周波数分析結果は周波数分解能ごとの飛び飛びの値となります。図3は少々大げさに描いていますが、離散フーリエ変換では真なる周波数成分のピーク値を表していない場合があります。この辺りの詳細については、実験モーダル解析を取り上げる際に述べたいと思います。

図3　離散フーリエ変換結果と真なる周波数成分［クリックで拡大］

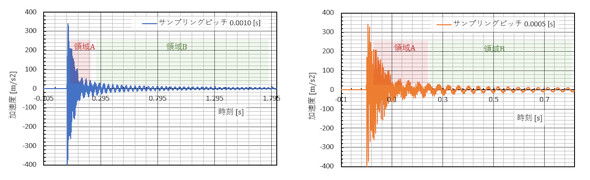
　図4に、図3と同じデータですがサンプリングピッチを半分にした際の振動加速度の時刻歴波形と周波数分析結果を示します。ここで“周波数成分のピーク値が倍になっている”ことにお気付きでしょうか。

図4　振動加速度の時刻歴波形と周波数分析結果：サンプリングピッチ 0.0005［s］［クリックで拡大］

　図5に時刻歴波形を並べてみました。離散フーリエ変換はsinとcosを掛けて、積分ではなく総和を取ることでした。sinとcosを掛ける相手は信号波形ですが、領域Bの信号はほとんどゼロなので総和はゼロです。領域Aには信号があり、サンプリングピッチ0.0005［s］の領域Aの長さが倍の長さです。ここの信号値とsinとcosを掛けて総和を取ったものが周波数分析結果になるので、領域Aの長さが異なれば両者の周波数分析結果は異なる値になります。

　「周波数分析とは単なる総和を取ることだ」と理解してもらえれば、全く同じ波形でもサンプリングピッチが変わると周波数成分のピーク値がコロコロ変わることが分かると思います。というわけで、FFTアナライザのピーク値の大小で一喜一憂する必要はなくなります。振動の大きさは時刻歴波形で評価すべきです。

図5　sinとcosを掛けて総和を取る対象［クリックで拡大］

周波数成分のピークの裾野に意味はあるのか？

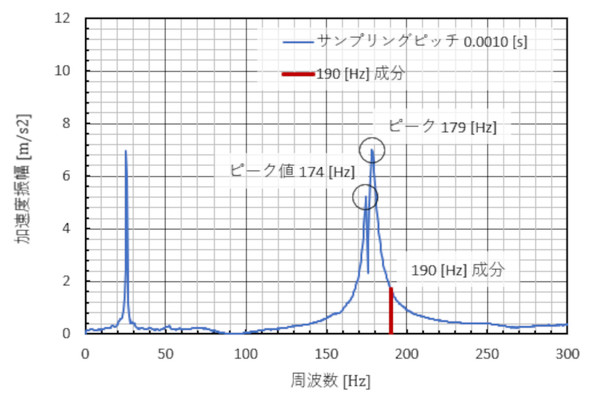
　図6に振動加速度の周波数分析結果を示します。174［Hz］成分と179［Hz］成分は存在することが分かります。しかし、190［Hz］成分の振幅は1.8［m/s²］なのですが、これは本当に存在するのでしょうか。

図6　振動加速度の周波数分析結果［クリックで拡大］

　連載第4回で、次式で信号f（t）にいろいろな周波数のsin波を掛けて総和を取りました。結果を表1に再掲します。

式1

表1　いろいろな周波数のsin波を掛けて積分した結果［クリックで拡大］

　では、101［Hz］のsin波を掛けた場合はどうなるのかというと、そう簡単にゼロにはならず、0.009924［-］となりました。総和は100［Hz］から離れるほどゼロに近づきます。図6の裾野である190［Hz］成分は、信号f（t）に190［Hz］のsin波を掛けて総和を取ったものの、結局ゼロにならなかっただけなのです。

　図6のように、179［Hz］成分のすぐ近くにある174［Hz］は元の信号に含まれている成分ですが、周波数分析結果の裾野はそのように周波数成分が元の信号に含まれているわけではなく“単に総和がゼロにならなかった結果”です。

　FFTアナライザの多くはデシベル表示（縦軸対数表示）が可能で、裾野が強調されて表示されますが、それをうのみにする必要はないようです。しかし、自然現象には本当にその周波数成分が存在していることがあり得るので、全ての測定結果に前述したことが当てはまるわけではありません。