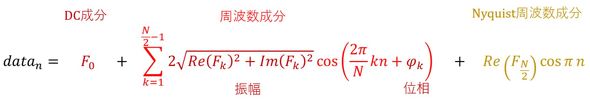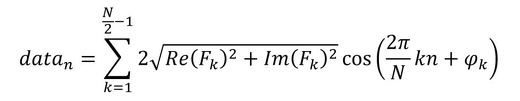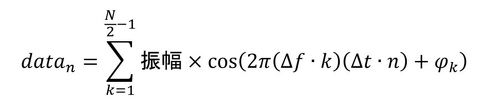Excelを使って周波数分析をやってみよう!:CAEと計測技術を使った振動・騒音対策(5)(1/5 ページ)
“解析専任者に連絡する前に、設計者がやるべきこと”を主眼に、CAEと計測技術を用いた振動・騒音対策の考え方やその手順を解説する連載。連載第5回では、測定データをExcelに取り込んで周波数分析を行う。
振動対策と騒音対策では、横軸を周波数として取り扱うことが常とう手段です。そして、USBポートにつなぐだけでPCがデジタルオシロスコープになる廉価なセットが普及しています。今回は測定データを「Excel」に取り込んで「周波数分析」をしてみます。
測定時間刻みΔt、データ数N、周波数分解能Δf
マクロ付きExcelファイルで周波数分析をする前に、測定時間刻みΔt、データ数N、周波数分解能Δfなどをはっきりさせておきましょう。測定時間刻みΔtは「サンプリングピッチ」とも呼ばれます。「高速離散フーリエ変換」では、データ数Nは2の累乗数でなければなりません。つまり、Nは256、512、1024、2048などです。筆者が若いころに使っていた「FFTアナライザ」の価格は2000万円以上もして、Nは512点だったと記憶しています。今となっては、Nはいくらでも多くできますが、当時はN=512点でも十分でした。
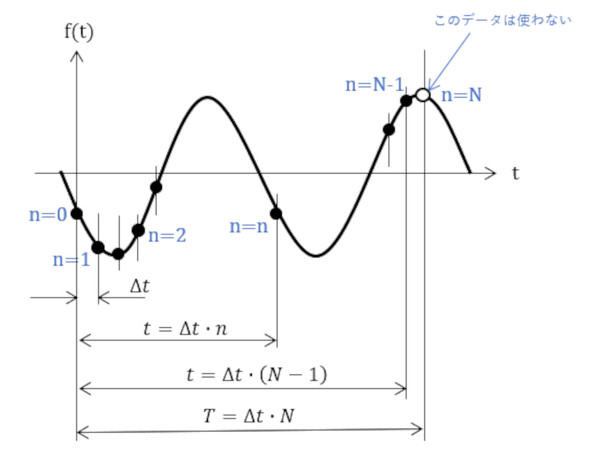
サンプリングピッチΔtでN個のデータを取得したとしましょう。図1の黒丸(●)の位置のデータです。
測定された物理量は時間の連続関数f(t)ですが、取得したデータはN個の離散データdatanとなり次式の関係があります。
「離散フーリエ変換」して得られる値をNで割ったものが振幅Fkですが、それぞれの振幅F0、F1、F2、F3……の周波数を求めましょう。「離散フーリエ逆変換」は次式で表されます。
少々長くなりますが、式2を変形すると次式になります。
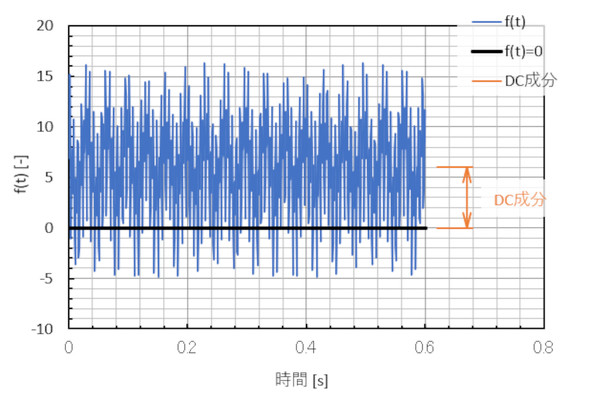
式3のF0はDC成分(直流成分)で、図2に示したように波形がゼロ点からオフセットしている量です。騒音計の電圧出力と加速度ピックアップのアンプはDC成分を出力しないので、これは考える必要はありません。最後のNyquist(ナイキスト)周波数成分は少々邪魔な項です。ちょうどNyquist周波数と一致する成分は後述する理由により観測できないため、この項も無視しましょう。
周波数成分の項に注目します。Σ記号が式2ではk=N−1までの総和だったのですが、式3ではk=N/2−1までの総和に変わっていますし、ルート記号の前に2が付いています。これは、離散フーリエ変換した振幅Fkについて以下の関係があるために、等しいものをひっくるめたためです。
Fkは複素数なので、Re(Fk)はFkの実数部、Im(Fk)はFkの虚数部です。無視しようといった項を除くと離散フーリエ逆変換は次式となります。位相Φkは、sinとcosの合成の結果出てきた位相角です。
式5から、元の信号はたくさんのcos波の総和で表すことができるということになります。それぞれのcos波の周波数をfkとしましょう。元の信号は次式でも表すことができます。
周波数分解能をΔfkとすると、k番目の周波数fkは「fk=Δfk×k」であり、時刻tは「t=Δt×n」なので、式6は次式となります。
ここで、式5と式7のcosの中は等しいこととします。
図1において、測定時間TはΔtNなので、周波数分解能とk番目の周波数fkは次式となります。
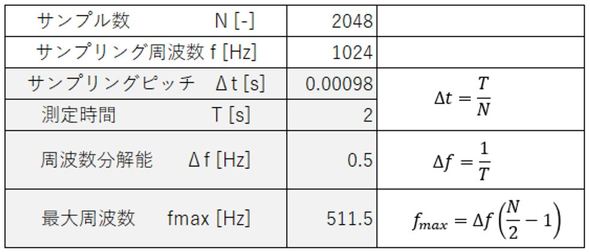
これらの関係は重要なので、表1に例を示します。自分で決める量はサンプル数とサンプリング周波数だけとなります。
Copyright © ITmedia, Inc. All Rights Reserved.