クーラン数と流体解析：初心者のための流体解析入門（7）（2/2 ページ）

流体解析をテーマに、入門者や初学者でも分かりやすくをモットーに、その基礎を詳しく解説する連載。今回は解析の安定性、そして解析精度や効率にも関わる「クーラン数」について取り上げる。

[水野操 mfabrica合同会社 社長／3D-GAN，MONOist]

大きな時間ステップは誤差の原因に

　さらに、現時点から未来の挙動を考える際、大きな時間ステップは誤差の原因にもなり得ます。非線形性があまりなく、また時間的な変動もあまりなければ、時間ステップの大きさはそれほど影響しないと考えられます。しかし、変動が非常に大きければ、大きな時間ステップは誤差を生む原因になり得ます。

　ちょっと違うかもしれませんが、天気予報をイメージしてみてください。最近、スマートフォンのお天気アプリなどで、会員が入力する現在地の天候情報をベースに、各地の詳細な天気を可視化するものがあります。こうした情報から非常に短期的な未来の天気をある程度正確に予測することは可能ですが、例えば、3カ月の長期予報となると予測確度は相当下がると考えられます。天気そのものが、とても非線形性の強い現象だからかもしれませんが、基本的に時間の間隔は短い方が正確です。

　その判断に使えるのが、クーラン数です。クーラン数が1かそれ以下で十分に現実的な時間で計算できるのであれば、それが最適といえます。しかし、現象によっては長い時間を計算する必要がある場合もあります。

　例えば、以前、筆者が行ったある火災絡みの計算では、数時間単位の計算をする必要がありました。小さいクーラン数の方がよいのは承知しつつも、そのときはクーラン数を10で計算しました。

　陰解法を使って計算する場合、現実的な計算時間に解析を収めることを考慮しつつも、精度の良い計算が実現できるようクーラン数を考える、あるいはそのクーラン数をベースに時間ステップを考えることが効率的な解析につながるのではないでしょうか。

クーラン数の大きさによる違いを検証

　以下、連載第2回で定常解析を実施したモデルに対し、非定常解析を行ったものを示します。

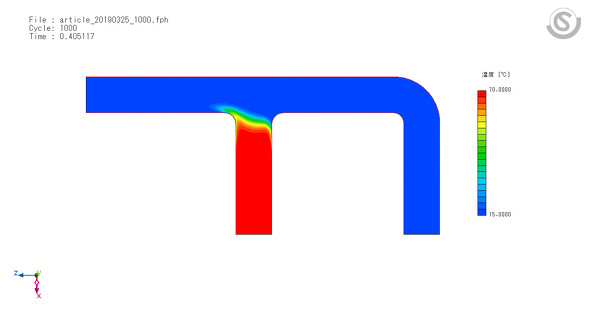
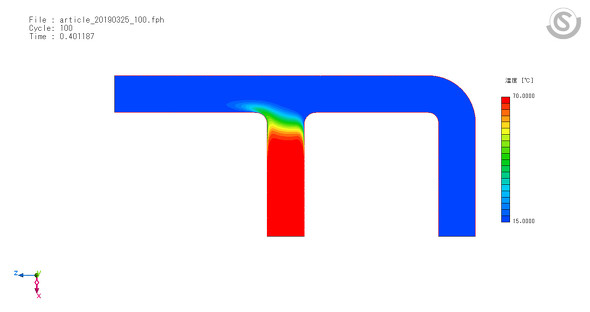
　クーラン数1で解析した場合、1000サイクルの解析を行っても、0.4秒分の解析しか行えず、定常に至るまでさらに解析を行う必要があることが分かります（図3）。一方、クーラン数10で解析した場合、0.4秒段階の結果はクーラン数1で行ったものとほぼ同様であり、また1000サイクル以内で、定常状態に至るまでの経過時間も把握できます（図4）。

図3　連載第2回の定常解析を非定常で実施。クーラン数1で1000サイクル終了時にスタートから約0.4秒。まだ定常状態には至っていない［クリックで拡大］

図4　クーラン数10で実施。100サイクルで約0.4秒。クーラン数1の結果とほぼ同様［クリックで拡大］

　確かに、クーラン数1ではより細かく挙動を追うことはできますが、この解析に関する限り、その詳細度はあまり意味のあるものではありませんでした。ただし、この解析の場合、クーラン数を大きくしても、全体像を把握する意味が十分にあるといえそうです（図5）。

図5　クーラン数10で解析した際、開始から約1.5秒（385サイクル）で定常解析とほぼ同様の結果に達している［クリックで拡大］

（次回に続く）

Profile

水野 操（みずの みさお）

1967年生まれ。mfabrica合同会社 社長。ニコラデザイン・アンド・テクノロジー代表取締役。3D-GAN理事。外資系大手PLMベンダーやコンサルティングファームにて3次元CADやCAE、エンタープライズPDMの導入に携わった他、プロダクトマーケティングやビジネスデベロップメントに従事。2004年11月にニコラデザイン・アンド・テクノロジーを起業し、オリジナルブランドの製品を展開。2016年に新たにmfabrica合同会社を設立し、3D CADやCAE、3Dプリンタ関連事業、製品開発、新規事業支援のサービスを積極的に推進している。著書に著書に『絵ときでわかる3次元CADの本』（日刊工業新聞社刊）などがある。