クーラン数と流体解析:初心者のための流体解析入門(7)(1/2 ページ)
流体解析をテーマに、入門者や初学者でも分かりやすくをモットーに、その基礎を詳しく解説する連載。今回は解析の安定性、そして解析精度や効率にも関わる「クーラン数」について取り上げる。
解析の安定性、そして解析精度や効率にも関わる「クーラン数」
伝熱解析や熱流体解析などを行う場合、最終的な状態(無限の時間後の状態)を求める定常解析と、時間を追ってその変化の経過を求める過渡解析、あるいは非定常解析があります。時間ごとの変化を追い掛ける解析に関しては、構造解析でいう動解析などもそれに該当します。
さて、そのような変化を追い掛ける解析で問題になるのが“計算の安定性”です。構造物の衝撃解析にせよ、流体解析にせよ、往々にして非常に強い非線形性を持つモデルを解く必要があります。今回は、そのような解析の安定性に関わる内容を取り上げます。
何らかの形で動的構造解析や、流体解析に触れたことがあるという人は、「クーラン数」という言葉を聞いたことがあるかもしれません。このクーラン数は、解析の安定性、さらには解析精度や効率にも関わってくる重要な要素です。
「クーラン条件」とは?
構造解析でも流体解析でも、私たちが普段使用する商用ソフトウェアでは、「メッシュ」によって解析空間を離散化したモデルで表現します。そのような離散化したモデルにおいて、波動を扱う場合に必要な条件が「クーラン条件」です。
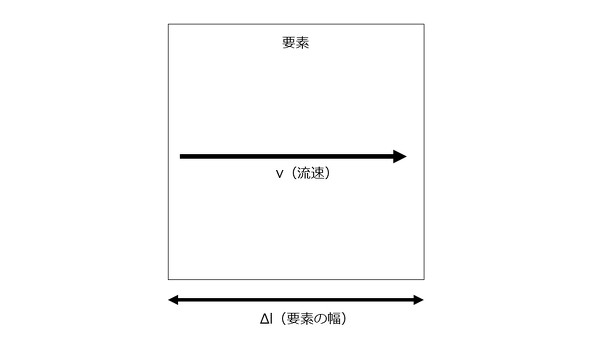
運動方程式の解を求める場合、ある時間ステップ「Δt」を用いるわけですが、そのときの「Δt」は、実際の波動が隣の節点(あるいは格子)に到達するまでの時間よりも小さな時間ステップでなくてはなりません。もっと簡単に言うと、流体解析における1ステップの時間幅で流れが移動する距離は、要素1個分の距離よりも短くなければならない、ということです。
クーラン数は、以下の式で表現できます(式1)。
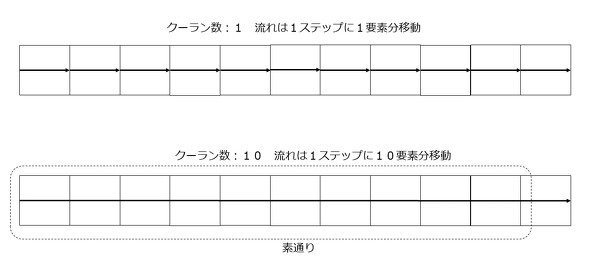
つまり、クーラン条件の定義からいくと、安定した解析をするためには“クーラン数は、1よりも小さい必要がある”ということです。
これは、特に「陽解法」で数値計算を行うプログラムで重要になってきます。クーラン数が1以上になる条件を与えてしまうと、情報伝達のスピードが実現象のスピードに追従できなくなり、発散してしまいます。Δtの値は、メッシュの要素の大きさ、あるいは格子の大きさにも依存するので、式1のΔlが小さければ(=メッシュが細ければ)、Δtもさらに小さくする必要があります。つまり、解析する現象の全体の時間的な長さと、モデル中のメッシュの大きさによって、解析全体に必要とされるステップ数は変わってきます。
もっとも、このクーラン数が数値計算上の“安定性の条件”とされるのは、陽解法に対してです。「陰解法」の場合、クーラン数の制約を受けずに計算を実行できます。
陽解法と陰解法
陽解法と陰解法については、説明すると長くなるので詳細は割愛しますが、陽解法は既知の現在の値のみをベースに未来を予測するため、計算式は容易で、マトリックス(連立一次方程式)を解く必要がないので計算は軽くなります。その代わり、安定した計算をするためには、時間ステップを非常に短くする(クーラン数を小さくする)必要があります。このような特徴から、構造解析などでは衝撃解析のようなコンマ数秒以下で、大きな変形(つまり、強い非線形性を持つ変形)が伴う現象の解析プログラムなどで採用されています。
一方、陰解法は真面目に連立一次方程式を解く必要があるため、解析の負荷は重たくなります。その代わり、時間ステップはクーラン数に関係なく大きなステップを取ることが可能です。つまり、ある現象を求める際、陽解法であれば100ステップ以上必要なところ、陰解法では極端なことを言えば1ステップで済むかもしれません。
しかし、陰解法だからといって時間ステップを(悪い意味で)適当に取ってよいというわけでもありません。そもそも、流体解析にせよ、構造解析にせよ、本来は連続体である物体を離散化していることに加え、時間の流れも本来は連続的に流れているものをある間隔で刻んでいるわけです。空間という観点で考えれば、基本的にメッシュは粗いよりも細かい方が、より正確に変位や応力といったものを捉えることができます。同様に、時間という観点から考えても、粗く刻むよりも細かく刻んだ方が挙動はより正確に得られます。
Copyright © ITmedia, Inc. All Rights Reserved.