幾何公差と寸法公差、測定方法は何が違うの？：寸法を実感する！ 測定講座（2）（3/3 ページ）

幾何公差や寸法測定の課題に対する幾つかの取り組みを紹介していく本連載。第2回は幾何公差と寸法公差での測定方法の違いについて解説する。

[木下悟志／プラーナー，MONOist]

幾何公差の測定方法

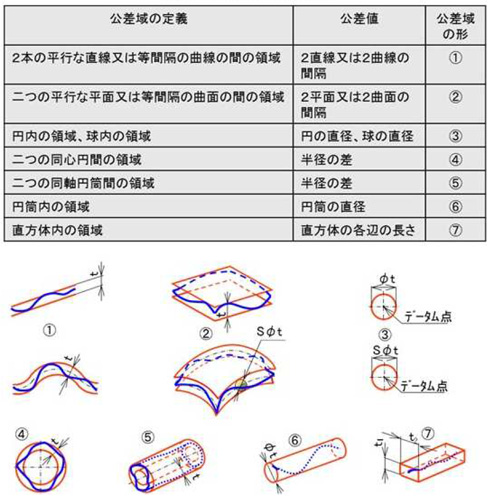
　さて、本連載の本題である測定に関してですが、先に述べたように寸法公差は2点間（1次元）測定なので、慣れ親しんだマイクロメーターやノギスなどの測定器で十分なのですが、幾何公差は図2に示すような2次元、3次元の公差域なので、2点間測定では事足りません。

図2：幾何公差の公差域（再掲）

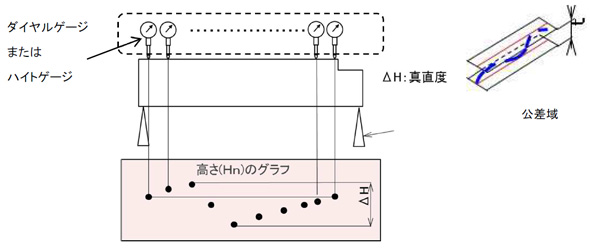
　まずは、真直度ですが、理想的には3次元測定機（CMM：Coordinate Measuring Machine）の接触式プローブにて多点測定を行い演算で求めるのがベストですが、原理を理解する上でも分かりやすい現実的な方法は、図6のようにダイヤルゲージ、ハイトゲージを用いての方法です。真直度は計測された値の最大値と最小値との差によって表します。直線方向の測定値となります。

図6：真直度の測定方法（ダイヤルゲージまたはハイトゲージ）

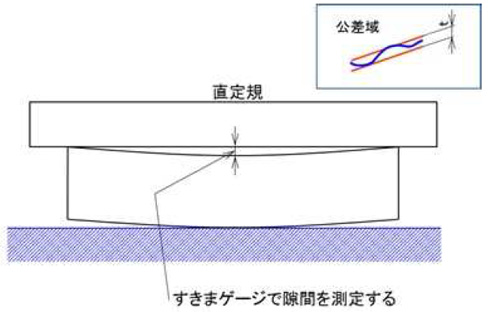
　また、現場レベルで簡便にできるのが直定規を用いた比較評価法です。実は、この方法はテンプレート（ひな型）を用いた検査方法として古くから活用されていて、「職人の目の鋭さ」で相当の高精度判定も可能です。特に高精度を達成できるのは、すき間ゲージではなく、目で見て光の透け具合から判定する方法です。

図7：真直度の測定方法（テンプレート）

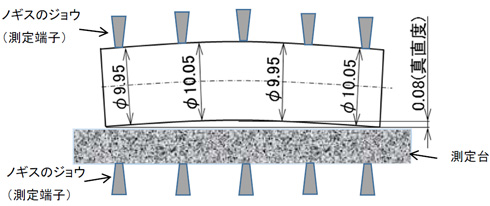
　マイクロメーターやノギスでは幾何公差の測定は不可能と言いましたが、工夫次第では可能です。例えば、図5のような形状の場合、図8のように平面度、平行度が保証された測定台を用いればノギスにて多点測定して求めることは可能です。ただし、板状のものは容易ですが、丸いものは固定に工夫が必要です。また、図8のように凸状のものは測定可能ですが、凹状のものはこの方法では難しいです。

図5：幾何公差併記の指示（再掲）

図8：ノギスによる真直度測定

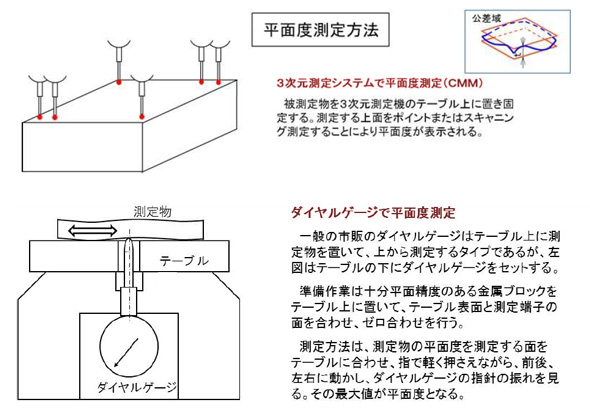
　次に平面度です。平面度もCMMを用いるのが一般的ですが、図9のような簡易測定器（特注品）でも測定は可能です。これも、凸状の場合は難しくなります。平面度の場合の測定値は、先の真直度の場合が直線上の値（1次元）であるのに対して平面上の値（2次元）となります。公差域の図も見比べてください。

図9：平面度の測定方法

　なお、真円度、円筒度、輪郭度の測定方法は次回以降で説明します。

---

　次回以降でも繰り返し述べますが、幾何公差の測定は理想的にはCMMに代表される3次元測定機に負うところが大きくなります。ですが設計者としては、そうだからと言って逃げることなく、信念を持って設計意図を明確にした公差指示をしていくことがより良い物づくりのためには重要です。

　ただ、その上で、製造してくださる方々、さらには測定してくださる方々、部品を調達してくださる方々との密接なコミュニケーションを図って、必要な測定機の整備、簡易的な測定方法の工夫をしていくことも重要で、自分のスキルアップにもつながります。　（次回へ続く）

⇒ 連載バックナンバーはこちら

木下悟志（きのした・さとし）

プラーナー 研修推進室 室長 シニアコンサルタント。セイコーエプソンにて34年間勤務。プラスチック応用の開発経験が長く、非球面レンズや超小型ギヤードモーターの開発から量産、マーケッティングまで経験した。また基幹商品であるウオッチ、インクジェットプリンタ、プロジェクターの要素開発にも長く関わった。近年は研究開発部門のマネジメントにおいて開発の意思決定や外部との共同研究・共同開発の方向付けをした。材料開発、機構設計、プロセス開発、計測技術開発と幅広い知見を持つ。2015年より、設計者の能力開発を支援するプラーナーのシニアコンサルタントとして、幾何公差と計測技術を融合したセミナーを創出し、担当している。大手企業をメインに多数の企業で連日セミナーを担当し、実践コンサルも行っている。

• 株式会社プラーナ―のWebページ